Découpe laser de pentagones qui pavent le plan
15 mai 2025 | Catégories: découpe laser, math | View CommentsEn janvier 2025, avec l'aide de David Renault, j'ai fait une nouvelle série de découpes lasers au fablab EirLab de l'ENSEIRB sur le thème des pavages par pentagones. Comme démontré par Michael Rao, il n'existe que 15 pavages pentagonaux possibles.
Voici quelques images de la découpe effectuée le 9 janvier 2025.
Un pentagone de type 7 découvert par Kershner en 1968:

Un pentagone de type 10 découvert par James en 1975:
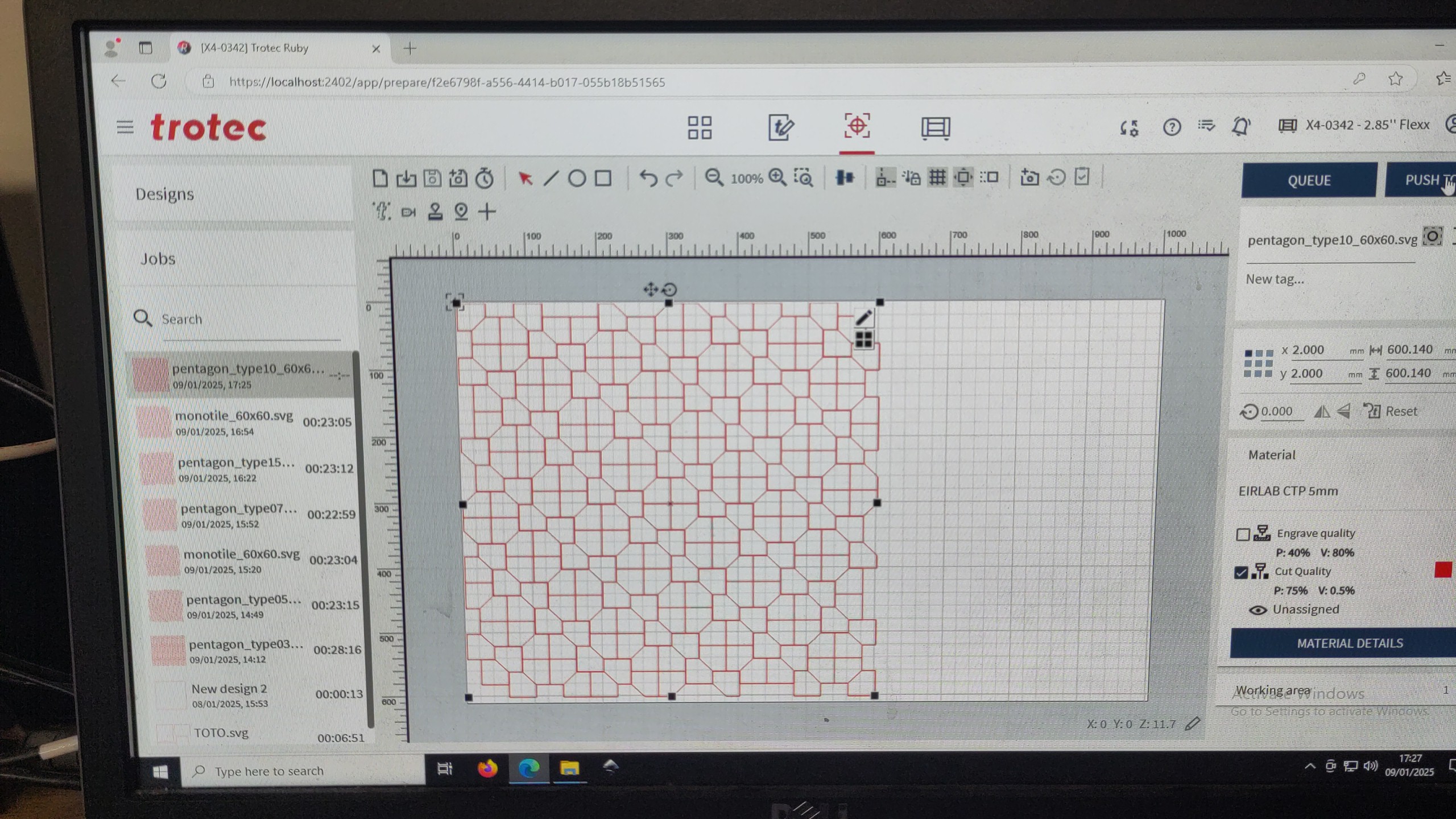

Le pentagone de type 15 découvert en 2015 par Jennifer McLoud-Mann, Casey Mann et David Von Derau, un étudiant de niveau licence en stage avec eux:

J'ai pu rencontrer Casey et Jennifer pour la première fois en 2017 à Montréal. Ils ont passé une année sabbatique à l'Université de Bordeaux en 2019-2020 via le programme Visiting Scholar de l'Université de Bordeaux, et cela a mené à une publication scientifique commune.
J'en ai aussi profité pour découper quelques tuiles chapeau apériodiques en plus:

Interventions dans les collèges et lycées en Gironde
Ces dernières années, sous l'invitation annuelle de Johanne Brengues, professeure au Lycée Kastler, j'ai développé un atelier sur la structure des flocons de neige et pavages apériodiques. Dans l'atelier d'une durée de 60 à 120 minutes, j'utilise des pièces en bois découpées au laser à l'ENSEIRB pour faire découvrir la science des pavages apériodiques et des quasicrystaux par la manipulation.
Pour l'année 2024-2025, j'ai soumis l'atelier suivant à l'Académie de Bordeaux dans le cadre de l'activité Des universitaires dans les classes.
Titre: Structure des flocons de neige et pavages apériodiques
Résumé: On dit que les flocons de neige sont tous différents. Pourquoi alors les branches d’un même flocon sont identiques? Dans cet exposé interactif, nous étudierons ces questions du point de vue des pavages du plan par des pièces de puzzle polygonales. Ces pièces se collent les unes aux autres comme le font en trois dimensions les molécules d’eau lors de la formation d’un flocon. En particulier, nous manipulerons des dizaines de copies d’un polygone à 13 côtés découvert en mars 2023. Les copies de ce polygone ont la propriété de paver le plan sans jamais se répéter. Nous utiliserons cet exemple pour discuter des pavages apériodiques du plan et de leurs propriétés. Public : tout niveau primaire + collège + lycée
J'ai été contacté par plusieurs collèges de la région pour faire cet atelier au printemps 2025:
- Collège Cassignol Bordeaux, 28 élèves de 3e, 7 janvier 2025
- Collège Jean Rostand, Casteljaloux, 3 classes de 6e, 16 janvier 2025
- Collège Olympe de Gouges, Vélines, 17 janvier 2025
- Village de maths, Collège Laure Gatet, Périgueux, 13 mars 2025
- Lycée Kastler, Talence, 15 mai 2025
- Collège Jean Zay, Cenon, 13 juin 2025
Les professeurs me disent que les pavages sont au programme du collège ce qui facilite les liens avec le sujet de l'atelier.
L'atelier en 2024-2025
Dans mes recherches, je m'intéresse à la combinatoire et à ses interactions avec les autres sciences. Par exemple, les atomes se combinent pour former des molécules stables en suivant des règles combinatoires simples. À l'état solide, les molécules peuvent se combiner pour former des structures ordonnées comme des crystaux ou même des flocons de neige.
La structure des flocons de neige est une science passionnante étudiée par Kenneth Libbrecht, professeur de physique au California Institute of Technology. Plusieurs questions naturelles peuvent-être posées par les élèves en voyant quelques images de flocons de neige:
- Pourquoi les flocons ont tous 6 branches?
- Pourquoi les branches d'un même flocon sont pareilles?
Après l'introduction sur la combinatoire et les flocons de neige, on passe à l'atelier. On divise la classe en petits groupes de 3 à 5 élèves. On attribue un atome (c'est-à-dire, plusieurs copies d'un même polygone) à chaque groupe. On demande aux élèves de trouver les molécules que l'atome peut créer en deux dimensions. On oriente les élèves à trouver des grandes molécules qui recouvrent des disques arbitrairement grand (on demande de recouvrir une feuille format A7, puis format A6, puis format A5, puis format A4).
Comme les pavages pentagonaux sont périodiques, nous démarrons l'atelier par l'exploration des pavages par l'un des 15 types de pentagones qui pavent le plan. Chaque groupe d'élèves se voit attribuer plusieurs copies d'une sorte de pentagones. Les élèves doivent explorer la combinatoire de la forme géométrique et faire des observations. Les découvertes des élèves sont publiées au tableau pendant l'atelier comme un article scientifique. Les résultats publiés peuvent être utilisés par les autres groupes à condition de les citer!
La notion d'apériodicité se transmet mieux après avoir compris la notion de pavages périodiques. La nouveauté pour mon atelier du printemps 2025 était de faire en sorte que les élèves découvrent d'abord des pavages périodiques non triviaux avant de considérer des pavages apériodiques. Cela permet de mieux expliquer la notion d'apériodicité.
Toutefois, avec une introduction de 15 à 20 minutes, l'atelier sur les pentagones nécessite presque la totalité du temps restant (30 minutes). Dans certains cas, un des groupes peut commencer l'étude de la pièce apériodique chapeau dans les 10 minutes restantes. Dans d'autres situations, je laisse un groupe choisir la pièce chapeau dès le début de l'atelier. Quand le temps le permet, on peut prévoir l'atelier en deux périodes de 60 minutes avec le même groupe. Cela permet d'explorer les pièces pentagonales périodiques, puis les pièces apériodiques tout en laissant du temps pour répondre aux questions des élèves.
Voici des fichiers qui rassemblent les images que j'utilise dans l'atelier sur les différents thèmes présentés.
Voici quelques liens pour en savoir plus:
Pour les collèges et lycées en dehors de Bordeaux et difficilement accessible en transport en commun, je remercie l'Université de Bordeaux pour le prêt d'une voiture.

On the bifurcation diagram proposed by Jang and Robinson
06 mai 2025 | Catégories: sage, math | View CommentsIn this blog post, we present a few remarks on the "bifurcation diagram" proposed by Jang and Robinson in [1] to describe the tilings associated to a set of 24 Wang tiles encoding Penrose tilings.
[1] Hyeeun Jang, E. Arthur Robinson Jr, Directional Expansiveness for Rd-Actions and for Penrose Tilings, arxiv:2504.10838
In particular, I believe that something is wrong in what the authors call the "bifurcation diagram" shown in Figure 10. But, as we illustrate below, it can be fixed easily by permuting some of the labels of the partition.
I saw Jang and Robinsion's bifurcation diagram for the first time during the talk "Remembering Shunji Ito" made by Robinson during the online conference dedicated to the memory of Shunji Ito on December 14, 2021. At that time, I was working on the family of metallic mean Wang tiles. This is why the bifurcation diagram shown by Robinson and extracted from Jang's PhD thesis got my attention right away, because it was looking very much like the Markov partition associated to the Ammann set of 16 Wang tiles, the first member of the family of metallic mean Wang tiles. As we illustrate below, Jang and Robinson's bifurcation diagram is a refinement of the Markov partition associated the Ammann set of 16 Wang tiles. This means that the 16 tiles Ammann Wang shift is a factor of the 24 tiles Penrose Wang shift. Also most probably the bifurcation diagram is a Markov Partition for the same associated toral ℤ2-action. But this needs a proof.
The content of this blog post is also available as a Jupyter notebook that can be viewed and downloaded from the nbviewer.
Dependencies
The computations made here depend on the modules WangTileSet, WangTiling, PolyhedronPartition, PolyhedronExchangeTransformation, PETsCoding implemented in the SageMath optional package slabbe over the last years in order to describe and study the Jeandel-Rao aperiodic tilings and the family of metallic mean Wang tiles.
Note that the package slabbe can be installed by running !pip install slabbe directly in SageMath:
sage: # !pip install slabbe # uncomment and execute this line to install slabbe package
Here are the version of the packages used in this post:
sage: import importlib sage: importlib.metadata.version("slabbe") '0.8.0'
sage: version() 'SageMath version 10.5.beta6, Release Date: 2024-09-29'
Jang-Robinson encoding of the Penrose 24 Wang tiles
We encode the 24 Wang tiles proposed by Jang and Robinson (Figure 9 of [1]) using alphabet {A, B, C, D, E, F, G, H, I, J} for the shapes:
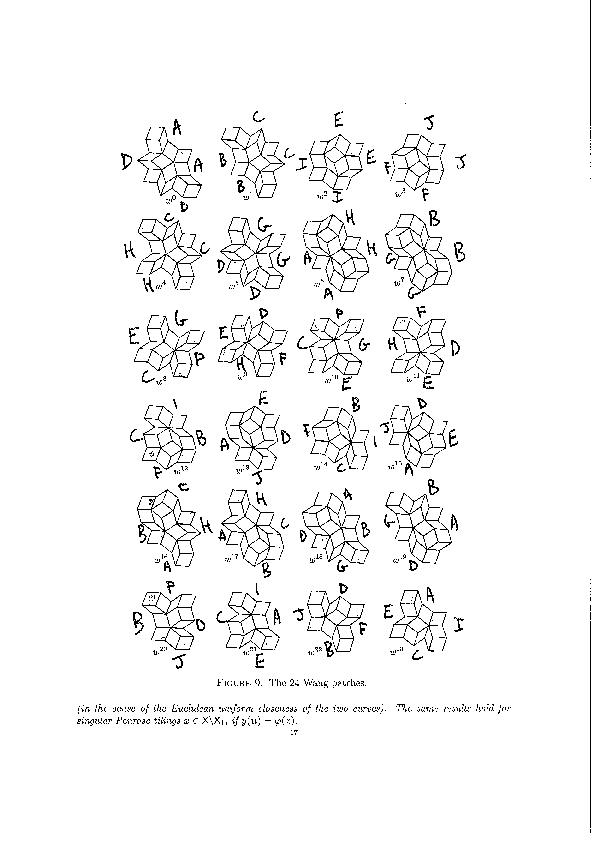
We define the 24 Wang tiles in SageMath:
sage: from slabbe import WangTileSet, WangTiling sage: tiles = ["AADD", "CCBB", "EEII", "JJFF", ....: "CCHH", "GGDD", "HHAA", "BBGG", ....: "FGEC", "FDEH", "GFCE", "DFHE", ....: "BICF", "DEAJ", "IBFC", "EDJA", ....: "HCBA", "CHAB", "BADG", "ABGD", ....: "DFBJ", "AICE", "FDJB", "IAEC"] sage: T0 = WangTileSet([tuple(str(a) for a in tile) for tile in tiles]) sage: T0 Wang tile set of cardinality 24
sage: T0.tikz(ncolumns=4)
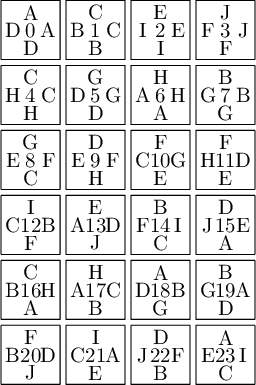
Constructing Jang-Robinson Bifurcation diagram as a polygonal partition
Below is a reproduction of Jang-Robinson bifurcation diagram shown in Figure 10 from arxiv:2504.10838

In this section, we construct this bifurcation diagram in SageMath as a polygonal partition.
sage: from slabbe import PolyhedronPartition
sage: z = polygen(QQ, 'z') sage: K = NumberField(z**2-z-1, 'phi', embedding=RR(1.6)) sage: phi = K.gen()
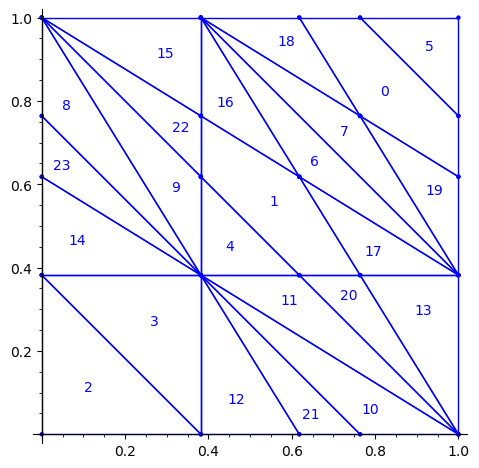
sage: square = polytopes.hypercube(2,intervals = 'zero_one') sage: P = PolyhedronPartition([square]) sage: P = P.refine_by_hyperplane([1/phi^3,-1,-1]) sage: P = P.refine_by_hyperplane([1/phi,-1,-1]) sage: P = P.refine_by_hyperplane([1,-1,-1]) sage: P = P.refine_by_hyperplane([1 + 1/phi,-1,-1]) sage: P = P.refine_by_hyperplane([1 + 1/phi^3,-1,-1]) sage: P = P.refine_by_hyperplane([1/phi,-phi,-1]) sage: P = P.refine_by_hyperplane([1,-phi,-1]) sage: P = P.refine_by_hyperplane([phi,-phi,-1]) sage: P = P.refine_by_hyperplane([1/phi^2,-1/phi,-1]) sage: P = P.refine_by_hyperplane([1/phi,-1/phi,-1]) sage: P = P.refine_by_hyperplane([1,-1/phi,-1]) sage: P = P.refine_by_hyperplane([1/phi,-1,0]) sage: P = P.refine_by_hyperplane([1/phi,0,-1]) sage: P = -P sage: P = P.translate((1,1)) sage: #P.plot() sage: P = P.rename_keys({0:5, 1:0, 2:18, 3:19, 4:7, 5:6, 6:16, 7:17, 8:1, 9:4, 10:15,11:9, sage: 12:22,13:23,14:8, 15:14,16:13,17:11,18:20,19:21,20:10, 21:12, 22:3, sage: 23:2}) sage: P.plot()
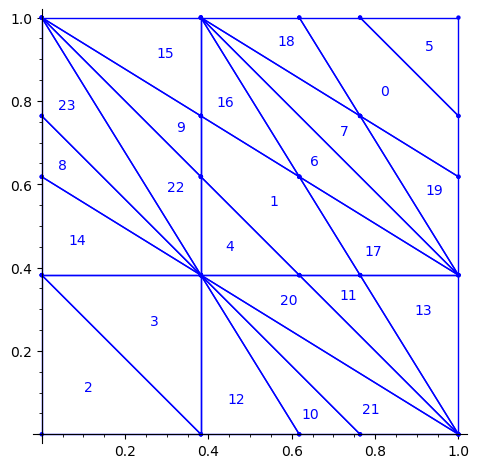
Our claim
We claim that the above bifurcation diagram from Jang-Robinson preprint is slightly wrong according to the choice of indices of the 24 Wang tiles made by Jang and Robinson and shown above. The following changes should be made in order to fix the partition:
- indices 9 and 22 should be swapped,
- indices 8 and 23 should be swapped,
- indices 11 and 20 should be swapped and
- indices 10 and 21 should be swapped.
Defining the toral translations in the internal space as PETs
We define the toral translations associated to the partition chosen by Jang-Robinson. The internal space is the 2-dimensional torus ℝ2 ⁄ ℤ2. It is represented as the unit square [0, 1)2. On this fundamental domain, a toral translation is a polygon exchange transformation.
Note that according to their choice,
- a unit horizontal translation in the physical space corresponds to a vertical translation by (0, φ) in the internal space,
- a unit vertical translation in the physical space corresponds to a horizontal translation by (φ, 0) in the internal space,
where φ is the golden mean.
Below, we follow their convention.
sage: from slabbe import PolyhedronExchangeTransformation as PET
sage: base = diagonal_matrix((1,1)) sage: R0e1 = PET.toral_translation(base, vector((0,phi))) sage: R0e2 = PET.toral_translation(base, vector((phi,0)))
We compute a 10×10 pattern obtained by coding the orbit of some starting point under the ℤ2-action R0.
sage: from slabbe.coding_of_PETs import PETsCoding
sage: coding_R0_P = PETsCoding((R0e1,R0e2), P) sage: pattern = coding_R0_P.pattern((.3,.4), (10,10)) sage: pattern = WangTiling(pattern, T0) sage: pattern.tikz()
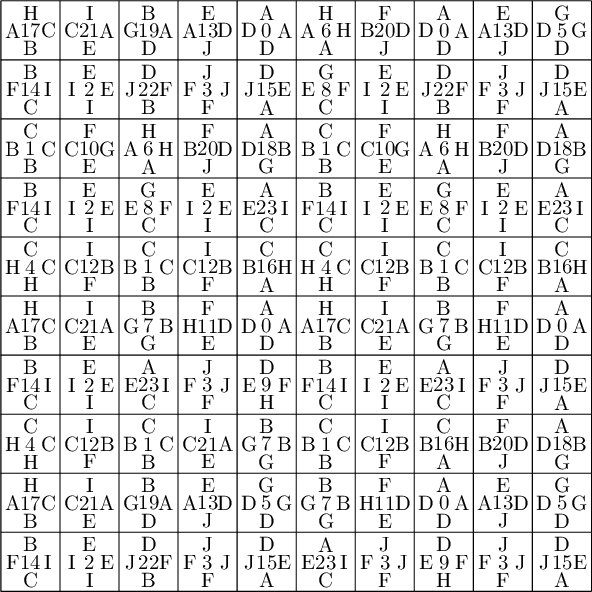
We observe that this pattern is not valid !!!
Let's fix the partition
We claim that the above pattern is wrong because something is wrong in the labelling of the atoms in the partition proposed by Jang and Robinson for the 24 Wang tiles encoding Penrose tilings.
Below, we fix the partition by swapping labels 8 and 23, 9 and 22, 11 and 20, 10 and 21:
sage: d = {i:i for i in range(24)} sage: d.update({8:23, 23:8, 9:22, 22:9, 11:20, 20:11, 10:21, 21:10}) sage: P1 = P.rename_keys(d) sage: P1.plot()
We compute a 10×10 pattern out of this updated partition P1:
sage: coding_R0_P1 = PETsCoding((R0e1,R0e2), P1) sage: pattern = coding_R0_P1.pattern((.3,.4), (10,10)) sage: pattern = WangTiling(pattern, T0) sage: pattern.tikz()
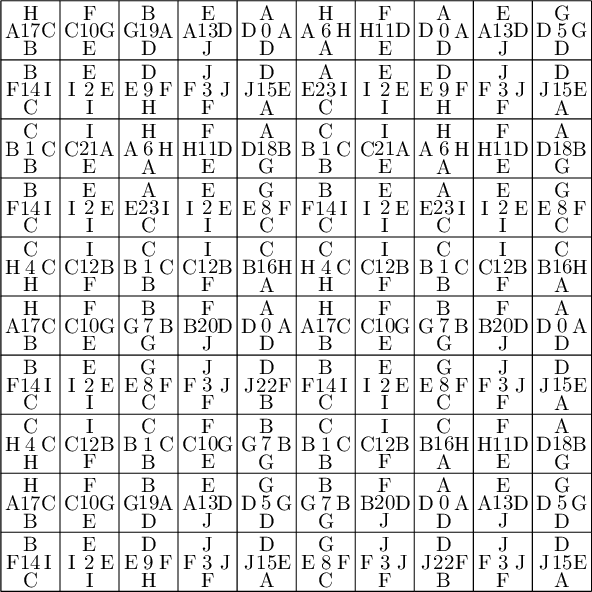
We observe that this pattern is valid !!!
Understanding the issue using edge label partitions
Let us try to understand the fix in terms of the Wang tiles east, north, west and south edge labels partitions induced by the original partition.
Indeed, since each atom of the partition corresponds to a Wang tile, we can deduce a partition of the unit square for the east labels (and respectively for the north, west and south labels) by merging two atoms in the partition if their east edge label is the same.
sage: def edge_label_partitions(partition, tiles): ....: EAST = partition.merge_atoms({i:tiles[i][0] for i in range(24)}) ....: NORTH = partition.merge_atoms({i:tiles[i][1] for i in range(24)}) ....: WEST = partition.merge_atoms({i:tiles[i][2] for i in range(24)}) ....: SOUTH = partition.merge_atoms({i:tiles[i][3] for i in range(24)}) ....: return EAST, NORTH, WEST, SOUTH sage: def draw_edge_label_partitions(partition, tiles): ....: EAST, NORTH, WEST, SOUTH = edge_label_partitions(partition, tiles) ....: L = [EAST.plot() + text('EAST', (.5,1.05)), ....: NORTH.plot() + text('NORTH', (.5,1.05)), ....: WEST.plot() + text('WEST', (.5,1.05)), ....: SOUTH.plot() + text('SOUTH', (.5,1.05))] ....: return graphics_array(L, nrows=2)
This is what we get using the partition proposed by Jang and Robinson for the 24 Wang tiles encoding Penrose tilings:
sage: draw_edge_label_partitions(P, T0)
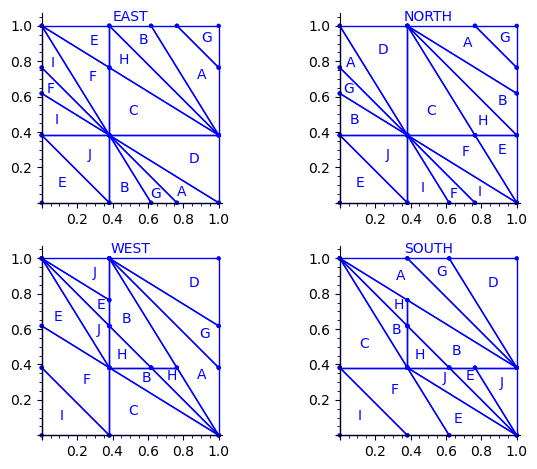
Here are some observations which are normal:
- partitions NORTH and EAST are symmetric under a reflexion by the positive diagonal (remember that the tile set is symmetric under the positive diagonal)
- partitions WEST and SOUTH are symmetric under a reflexion by the positive diagonal (remember that the tile set is symmetric under the positive diagonal)
Here are some observations which are not normal:
- partitions WEST and EAST do not give the same area to the same index (in a Wang tiling, the frequency of a EAST label should be equal to the frequency of the same WEST label)
- partitions SOUTH and NORTH do not give the same area to the same index (in a Wang tiling, the frequency of a NORTH label should be equal to the frequency of the same SOUTH label)
- partitions EAST and WEST are not a translate of one another (idealy a horizontal translate)
- partitions SOUTH and NORTH are not a translate of one another (idealy a vertical translate)
Another indication that something may be wrong is:
- atoms B, H, E, J, A, G are not convex in the torus
This is not a necessity. Atoms are not convex in the Markov partition associated to Jeandel-Rao tilings [2]. But they are convex for the Ammann set of 16 Wang tiles and their generalization to metallic mean numbers made in [3,4]. Since Penrose tilings are closely related to Ammann A2 tilings, we may also expect to have simple convex atoms in each of the four edge label partitions.
Here is the area of each atom in each of the four partitions. We observe that only atoms C and D have the same area in each of the four partitions.
sage: def table_of_area_of_atom_in_east_north_west_south_partitions(partition, tiles): ....: columns = [] ....: labels = 'ABCDEFGHIJ' ....: EAST, NORTH, WEST, SOUTH = edge_label_partitions(partition, tiles) ....: for partition in [EAST, NORTH, WEST, SOUTH]: ....: d = partition.volume_dict() ....: column = [d[a] for a in labels] ....: columns.append(column) ....: header_row = ['EAST', 'NORTH', 'WEST', 'SOUTH'] ....: return table(columns=columns, header_row=header_row, header_column=['']+list(labels))
sage: table_of_area_of_atom_in_east_north_west_south_partitions(P, T0) │ EAST NORTH WEST SOUTH ├───┼────────────────┼────────────────┼────────────────┼────────────────┤ A │ 15/2*phi - 12 15/2*phi - 12 phi - 3/2 phi - 3/2 B │ phi - 3/2 phi - 3/2 15/2*phi - 12 15/2*phi - 12 C │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 D │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 E │ phi - 3/2 phi - 3/2 -11/2*phi + 9 -11/2*phi + 9 F │ -11/2*phi + 9 -11/2*phi + 9 phi - 3/2 phi - 3/2 G │ -8*phi + 13 -8*phi + 13 -3/2*phi + 5/2 -3/2*phi + 5/2 H │ -3/2*phi + 5/2 -3/2*phi + 5/2 -8*phi + 13 -8*phi + 13 I │ 5*phi - 8 5*phi - 8 -3/2*phi + 5/2 -3/2*phi + 5/2 J │ -3/2*phi + 5/2 -3/2*phi + 5/2 5*phi - 8 5*phi - 8
But, we observe that we can fix the partitions if we assume that the atoms C and D in the four partitions are correct. There is a unique translation sending atoms C,D in the partition WEST to the atoms C and D in the partition EAST. That translation should send the partition WEST exactly on EAST. Similarly for SOUTH and NORTH. This suggest a way to fix atoms B, H, E, J, A, G in the partition.
Fixed Edge labels partitions
Using the fixed partition, here is what we get.
sage: P1.plot()
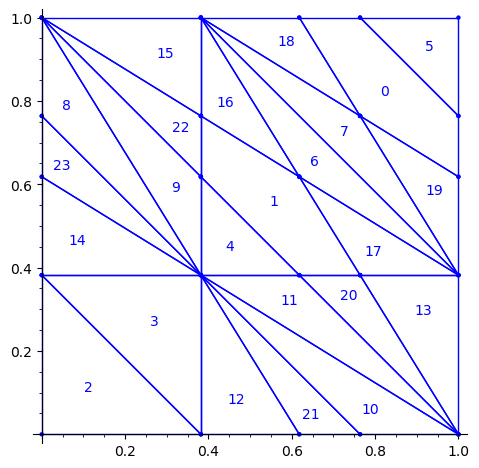
sage: draw_edge_label_partitions(P1, T0)
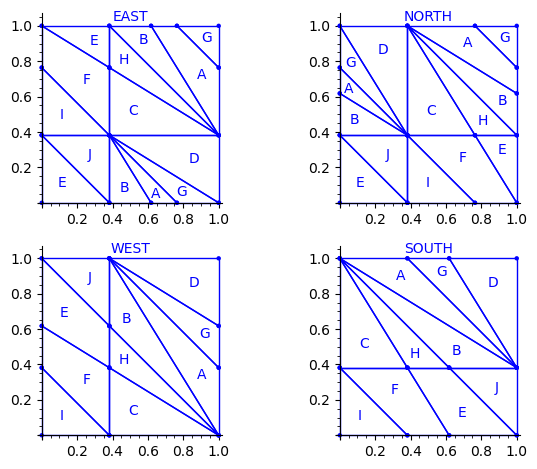
Now it looks good! As for the partitions associated to the metallic mean Wang tiles, the four partitions are isometric copies of the other ones (under toral translation or reflection).
sage: table_of_area_of_atom_in_east_north_west_south_partitions(P1, T0) │ EAST NORTH WEST SOUTH ├───┼────────────────┼────────────────┼────────────────┼────────────────┤ A │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 B │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 C │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 D │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 E │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 F │ phi - 3/2 phi - 3/2 phi - 3/2 phi - 3/2 G │ -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 H │ -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 I │ -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 J │ -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2 -3/2*phi + 5/2
sage: (phi-3/2).n(), (-3/2*phi + 5/2).n() (0.118033988749895, 0.0729490168751576)
Labels A, B, C, D, E and F all have the same frequency of ϕ − (3)/(2) ≈ 0.118.
Labels G, H, I and J all have the same frequency of − (3)/(2)ϕ + (5)/(2) ≈ 0.0729.
We check that frequencies sum to 1:
sage: 6 * (phi-3/2) + 4 * (-3/2*phi + 5/2) 1
Proposed partition for the encoding of the Penrose tilings into 24 Wang tiles
As done with the Markov partition associated to Jeandel-Rao aperiodic tilings, and for the Markov partition associated to the family of metallic mean Wang tiles, I think it is more natural to associate horizontal (vertical) translations in the internal space with horizontal (vertical) translations in the physical space. This way, the brain is less mixed up and the projections in the physical space π and in the internal space πint of the cut and project scheme are defined more naturally. This way the internal space and physical space can even be identified: this is the root of the do-it-yourself tutorial allowing the construction of Jeandel-Rao tilings [5]. See also my Habilitation à diriger des recherches written in English during Spring 2025 for more information [6].
First, we flip the partition P1 by the positive diagonal. This exchanges the role of x and y axis.
sage: P2 = P1.apply_linear_map(matrix(2, [0,1,1,0])) sage: P2.plot()
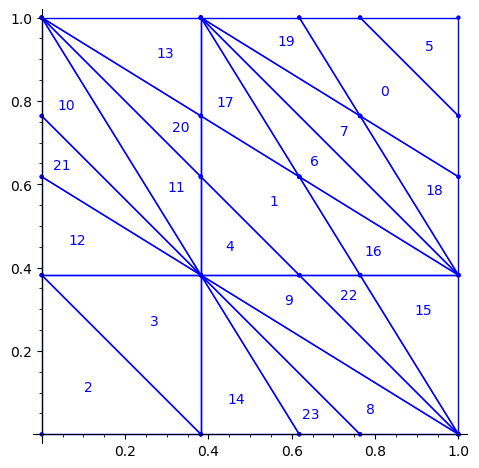
This allows to define the ℤ2-action R1 on the torus with horizontal and vertical translations for e1 and e2 respectively:
sage: base = diagonal_matrix((1,1)) sage: R1e1 = PET.toral_translation(base, vector((1/phi,0))) sage: R1e2 = PET.toral_translation(base, vector((0,1/phi)))
Then, we rotate the partition. This changes the origin of the partition. This change may be optional, but it makes the partition look closer to the partitions already studied in [2,3,4]. It simplifies the explanation of any relation between them (and there is one, see below!).
sage: P3 = R1e1(P2) sage: P3 = R1e2(P3) sage: P3.plot()
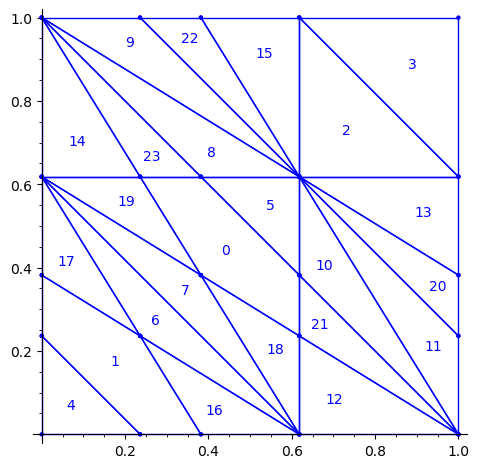
We observe that the partition P3 associated to the 24 Wang tiles encoding Penrose tiling is a refinement of the partition associated to the 16 Ammann tiles (see Figure 15 in [4] as the 16 Ammann tiles are equivalent to the n-th metallic mean Wang tiles when n = 1).
We compute a 10×10 pattern obtained by coding the orbit of some starting point under the ℤ2-action R1 using partition P3.
sage: from slabbe.coding_of_PETs import PETsCoding
sage: coding_R1_P3 = PETsCoding((R1e1,R1e2), P3) sage: pattern = coding_R1_P3.pattern((.3,.4), (10,10)) sage: pattern = WangTiling(pattern, T0) sage: pattern.tikz()
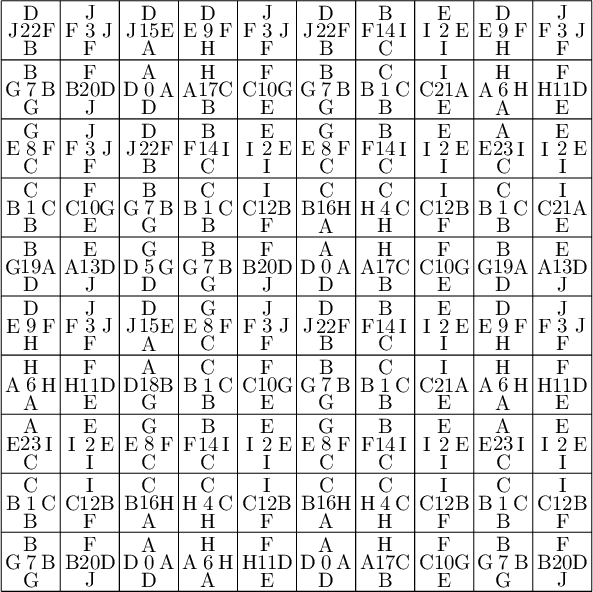
We are happy to see that the pattern is still valid after all the changes we have made!
sage: draw_edge_label_partitions(P3, T0)
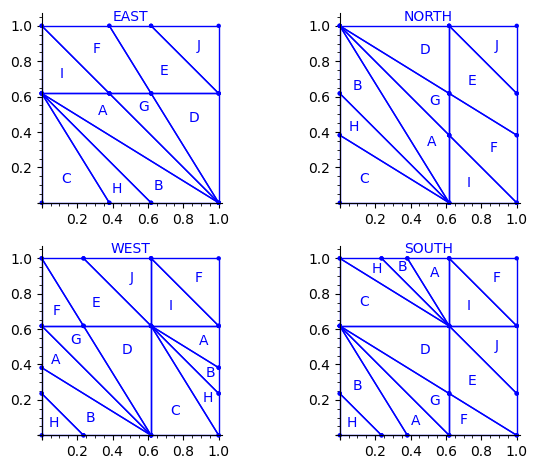
We observe that the EAST, NORTH, WEST and SOUTH partitions are a refinement of the EAST, NORTH, WEST and SOUTH partitions associated to the Ammann tiles partition (see Figure 15 in [4]).
The difference between the Ammann EAST and 24 Wang tiles Penrose EAST partition is the addition of two closed geodesics of slope -1 on the 2-torus passing through the origin and through the vertex (0, φ − 1).
It is possible that there is a clever way of including this information into the labels of the Wang tiles as we have done it for the family of metallic mean Wang tiles. Possibly, we need to use 4-dimension vectors for the tile labels instead of 3-dimensional integer vectors. This remains an open question.
Wang tiles deduced from the partition and ℤ2-action
We check that the Wang tiles computed from the partition P3 and ℤ2-action R1 is the original set of 24 Wang tiles defined by Jang and Robinson.
See Proposition 8.1 in [2].
sage: T = coding_R1_P3.to_wang_tiles() sage: T.tikz()
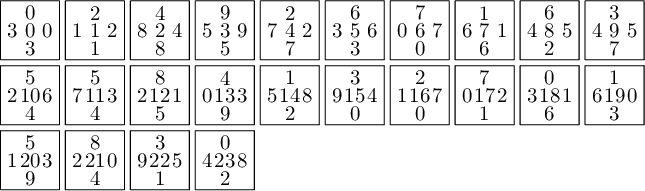
sage: T.is_equivalent(T0, certificate=True) (True, {'3': 'D', '0': 'A', '6': 'G', '1': 'B', '7': 'H', '2': 'C', '8': 'I', '4': 'E', '5': 'F', '9': 'J'}, {'3': 'D', '0': 'A', '6': 'G', '1': 'B', '7': 'H', '2': 'C', '8': 'I', '4': 'E', '5': 'F', '9': 'J'}, Substitution 2d: {0: [[0]], 1: [[1]], 2: [[2]], 3: [[3]], 4: [[4]], 5: [[5]], 6: [[6]], 7: [[7]], 8: [[8]], 9: [[9]], 10: [[10]], 11: [[11]], 12: [[12]], 13: [[13]], 14: [[14]], 15: [[15]], 16: [[16]], 17: [[17]], 18: [[18]], 19: [[19]], 20: [[20]], 21: [[21]], 22: [[22]], 23: [[23]]})
A do-it-yourself polygonal partition to construct Jeandel-Rao tilings
05 avril 2024 | Mise à jour: 07 février 2025 | Catégories: découpe laser, math | View CommentsIn 2015, Emmanuel Jeandel and Michael Rao discovered a very nice set of 11 Wang tiles which can be encoded geometrically into the following set of 11 geometrical shapes:

Jeandel and Rao proved that you may tile the plane with infinitely many translated copies of these tiles, but never periodically:

There is an easy way to construct Jeandel-Rao tilings from a well-chosen polygonal partition of the plane.
This is the polygonal partition:
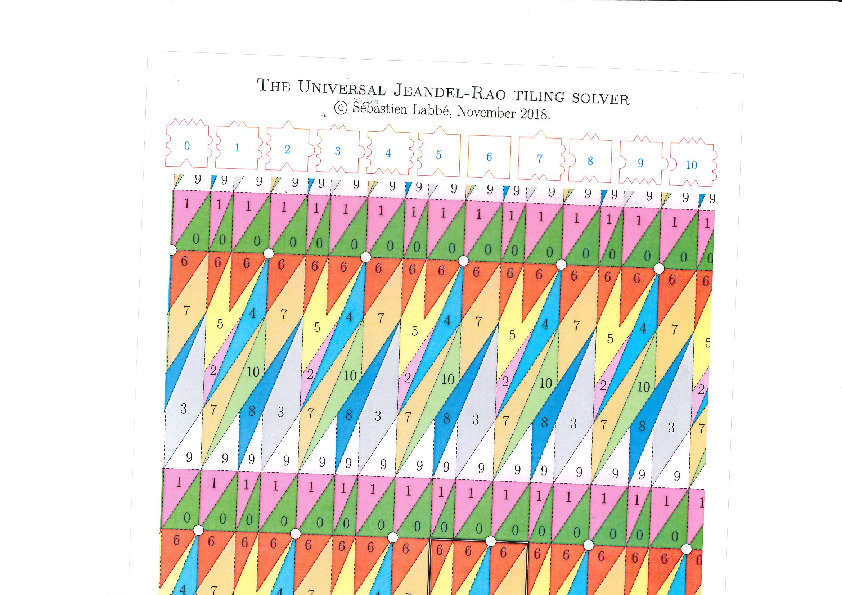
A lattice, represented below by the set of intersection of two perpendicular set of gridlines, is placed at a random position on top of the partition:

Each point of the lattice can be associated to an index from 0 to 10 according to which polygon of the partition it falls in. This defines a configuration of indices associated to each integer coordinate:
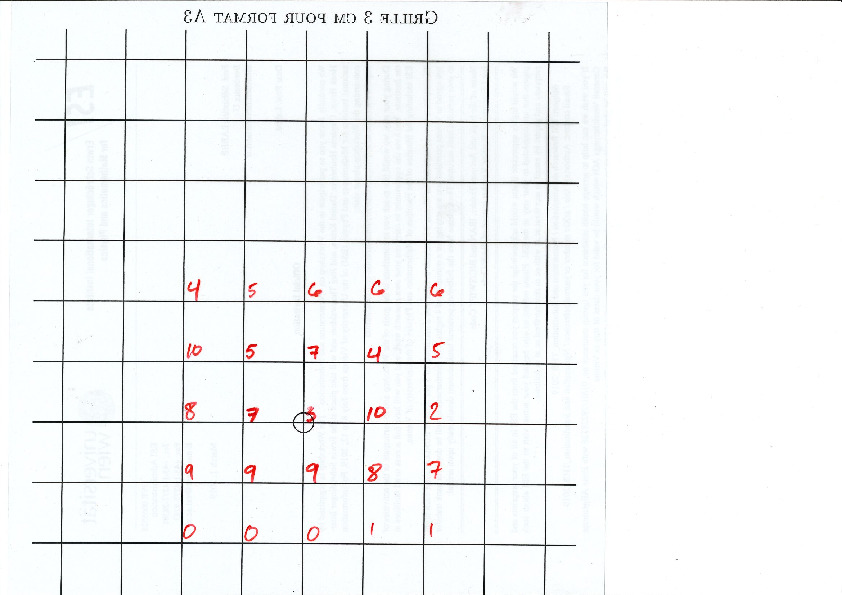
This procedure can be done all the way up to infinity. The chosen placement of the lattice defines a valid tiling of the plane with Jeandel-Rao tiles!

Since the size of the fundamental domain of the polygonal partition is irrational (width is golden mean, height is golden mean + 3, while the distance between two parallel gridlines is 1 unit), the generated configuration must be non-periodic.
It was a pleasure for me to do illustrate this to Emmanuel Jeandel during the workshop Multidimensional symbolic dynamics and lattice models of quasicrystals at CIRM in April 2024 in Marseille.

Do it yourself
Here are the files allowing to reproduce this experiment:
- A 33 x 19 rectangular valid patch of 627 tiles to use to cut a 1 meter x 60 cm wooden flat sheet (in svg format for laser cutting, pieces should have a side length of exactly 3 cm after the operation)
- The polygonal partition to be printed on a A3 paper (1 unit = 3 cm)
- The lattice \(\mathbb{Z}^2\) represented by gridlines 3cm apart to be printed on A4 paper (1 unit = 3 cm)
- The one-page Jeandel-Rao tiling solver tutorial
Alternate files for laser cutting the tiles
I first cut those tiles in August 2018 before a conference in Durham with the help of David Renault. We made more of them in June 2019. Each time David does some changes to the file that I provide to him with InkScape. Here are three alternate files for laser cutting the tiles.
Frequency of tiles
The frequency of tiles in a Jeandel-Rao tilings is computed below from the relative area in the associated polygonal partition. Tile #2 is the least frequent (around 2.55%) while tile #7 is the most frequent (around 15%):
sage: from slabbe.arXiv_1903_06137 import jeandel_rao_wang_shift_partition sage: P0 = jeandel_rao_wang_shift_partition() sage: V = P0.volume() sage: tile_frequency = {a:v/V for (a,v) in P0.volume_dict().items()} sage: rows = [(a, tile_frequency[a], tile_frequency[a].n(digits=3)) for a in range(11)] sage: table(rows, header_row=['tile', 'frequency', 'frequency (numerical approx)']) tile frequency frequency (numerical approx) ├──────┼───────────────────┼──────────────────────────────┤ 0 -1/22*phi + 2/11 0.108 1 -1/22*phi + 2/11 0.108 2 9/22*phi - 7/11 0.0255 3 -1/22*phi + 2/11 0.108 4 2/11*phi - 5/22 0.0669 5 -5/11*phi + 9/11 0.0828 6 -1/22*phi + 2/11 0.108 7 -3/11*phi + 13/22 0.150 8 2/11*phi - 5/22 0.0669 9 -1/22*phi + 2/11 0.108 10 2/11*phi - 5/22 0.0669
When I construct a bag of 50 tiles of the Jeandel-Rao tiles, I follow the above tile frequencies. It yields:
sage: [(tile_frequency[a]*52).n(digits=3) for a in range(11)] [5.63, 5.63, 1.33, 5.63, 3.48, 4.30, 5.63, 7.78, 3.48, 5.63, 3.48] sage: [round(a) for a in _] [6, 6, 1, 6, 3, 4, 6, 8, 3, 6, 3] sage: sum(_) 52
Discussion
The construction of valid tilings with Jeandel-Rao tiles from a polygonal partition is a generalization of a well-known phenomenon in one dimension, namely, the fact that Sturmian sequences of complexity \(n+1\) are coded by irrational rotations. For example, here is an easy way to construct Sturmian sequences using a partition of the line into two intervals of different lengths. Similarly as above, every point from a set of equidistanced points is coded by letter A or B according to which of the two intervals it falls in.

The question that one may ask is whether all Jeandel-Rao tilings can be constructed from such a starting point in the partition. For Sturmian sequences, the answer is yes and the starting point can be described using the Ostrowski numeration system and the continued fraction expansion of the slope defined from the ratio of frequencies of the letters in the sequence. In one dimension, the proof is thus based on the desubstitution of Sturmian sequences on the one hand, and the Rauzy induction of irrational rotations on the other hand.
The same approach can be performed for Jeandel-Rao tilings using 2-dimensional desubstitution of Wang tilings and 2-dimensional Rauzy induction of toral \(\mathbb{Z}^2\)-rotations. Surprisingly, the two totally different methods applied on two completely different objects lead to the same sequence of eventually periodic 2-dimensional substitutions. Thus, every Jeandel-Rao tiling that can be desubstituted indefinitely can be constructed from the coding of some starting point in the polygonal partition.
Unfortunately, not all Jeandel-Rao tilings can be desubstituted indefinitely because of the existence of a horizontal fault line breaking the substitutive structure. Some configuration have a biinfinite horizontal row of the same tile labeled 0 in them. This allows to slide the lower half of configuration along the fault line and the configuration remains valid. A conjecture is that the remaining configurations are rare (of probability zero according to any shift-invariant probability measure). More precisely, I believe that all of the problematic ones can be described by a pair of starting points on the bottom segment of the polygonal partition. During the sabbatical year of Casey Mann and Jennifer Mcloud-Mann in Bordeaux in 2019-2020, we tried hard to prove that conjecture without success. It seems to be a difficult problem. Instead we described the nonexpansive directions in Jeandel-Rao tilings which reminds of the behavior of Penrose tilings with respect to Conway worms, their resolutions and essential holes (annulus of tiles which can be completed uniquely outside of the annulus, but not inside).
Aperiodic tilings related to the Metallic mean
The structure of Penrose aperiodic tilings, Jeandel-Rao aperiodic tilings and the new aperiodic hat monotile are all related to the golden mean. Do all aperiodic tilings need to be related to the golden ratio? What other numbers can be achieved?
During the conference at CIRM, I presented my newest result split into two parts: for every positive integer \(n\), there exists an aperiodic set of \((n+3)^2\) Wang tiles whose tiling structure is associated to the \(n\)-th metallic mean number, that is, the positive root of the polynomial \(x^2-nx-1\). This new discovery extends the knowledge we have on aperiodic tilings beyond the omnipresent golden ratio. The talk was recorded on youtube and the written notes are available here.
Jean-René Chazottes et Marc Monticelli
During the conference at CIRM, I met Jean-René Chazottes and Marc Monticelli. They made me know about their interactive online books, the outreach mathemarium website and its online experiments. Also, the Open-Fabrik-Maths fablab in Nice, including some experiments involving aperiodic Wang tilings.
Introduction to Python/SageMath
27 juin 2023 | Catégories: sage, math | View CommentsOn Wednesday June 28th, 2023, I give short a Introduction to Python/SageMath as an online course organized by Pierre-Guy Plamondon in Mathematical Summer in Paris (MSP23) on WorkAdventure. Below is the material that will be presented or suggested.
Exercises:
- Install and open a Jupyter notebook and do the User Interface Tour in the help menu.
- Programming with Python. Here is a list of Jupyter notebooks to learn programming in Python: ProgrammingExercises.zip or ProgrammingExercises.tar.xz
- Reproduce the computations made by BuzzFeedNews in a github repository of your choice, for instance about the fentanyl and cocaine overdose deaths (2018) or about The Tennis Racket (2016).
- Solve some problems from the Project Euler. Project Euler contains more than 500 exercises that have to be solved with a computer
- Reproduce one or more images from the matplotlib library.
- Download the book Mathematical Computation with Sage by Paul Zimmermann et al. about the SageMath open source software. Reproduce the computations made in a section of your choice in the book.
- Visit https://ask.sagemath.org/questions/ and try to reproduce some of the best answers to questions of interest for you.
- Choose a section of your choice in the SageMath very large Reference Manual and reproduce the computations made in it.
When working on the above, two principles applies:
- Once you finished solving a notebook or a problem on Project Euler on your own you need to explain your solution to at least one other person (who has already solved the same notebook or problem).
- Once you reproduced the computation made by BuzzFeedNews, matplotlib image or some computation, you need to present and explain it to at least one other person.
Supplementary material:
- Experimenting with Dynamical systems in SageMath: DynamicalSystemExercices.zip
- Some more notebooks and exercices from this course given by Vincent Delecroix at AIMS in Rwanda (2016).
Découpe laser du chapeau, tuile apériodique découverte récemment
25 mai 2023 | Catégories: sage, slabbe spkg, math, découpe laser | View CommentsLe chapeau est une tuile apériodique découverte par David Smith, Joseph Samuel Myers, Craig S. Kaplan, et Chaim Goodman-Strauss le 20 mars 2023. Suite à un exposé donné le 26 mars au National Museum of Mathematics, la nouvelle s'est vite répandue. En effet, cette découverte a été mentionnée les jours suivants dans des blogues puis dans Le New York Times le 28 mars, Le Monde le 29 mars, puis The Guardian et QuantaMagazine le 4 avril. Un vidéo de 20 minutes, réalisé par Passe-Science et publié début le 3 mai, explique le résultat et son contexte.
Déjà des articles proposant des résultats plus approfondis sur la tuile par des experts du domaine sont parus sur arXiv en mai 2023. Ils interprêtent les pavages comme des coupes et projection de réseaux de dimension supérieure. Le deuxième propose même une partition de la fenêtre de l'espace interne, un peu comme pour les pavages de Jeandel-Rao, à la différence qu'ici la partition a des bords fractales ce qui est pour moi une grande surprise.
Comme je faisais une intervention dans l'école de mon garçon à Bègles le 3 mai et au Lycée Kastler de Talence le 4 mai, j'ai réalisé un projet de découpe laser sur la tuile apériodique afin de partager cette récente découverte.
La première question était de construire un pavage d'un rectangle assez grand avec la pièce apériodique. Pour ce faire, j'ai ajouté un nouveau module dans mon package optionel au logiciel SageMath.
Le module réalise une réduction à une instance du problème de la couverture universelle, qui peut être résolu dans SageMath en utilisant l'algorithme des liens dansants de Donald Knuth, les solveurs SAT ou les programmes d'optimisation linéaire (solveur MILP). Le code utilise le système de coordonnées défini dans le fichier validate/kitegrid.pdf qui se trouve dans le code source associé à l'article.
Voici un exemple de construction d'un pavage avec la tuile apériodique. Le calcul est fait dans le logiciel SageMath muni de la version de développement de mon package optionnel slabbe qui peut être installé avec la commande sage -pip install slabbe. Ici, j'utilise le solveur SAT Glucose, développé au LaBRI. On peut installer glucose dans SageMath avec la commande sage -i glucose.
sage: from slabbe.aperiodic_monotile import MonotileSolver sage: s = MonotileSolver(16, 17) sage: G = s.draw_one_solution(solver='glucose') sage: G.save('solution_16x17.png') sage: G
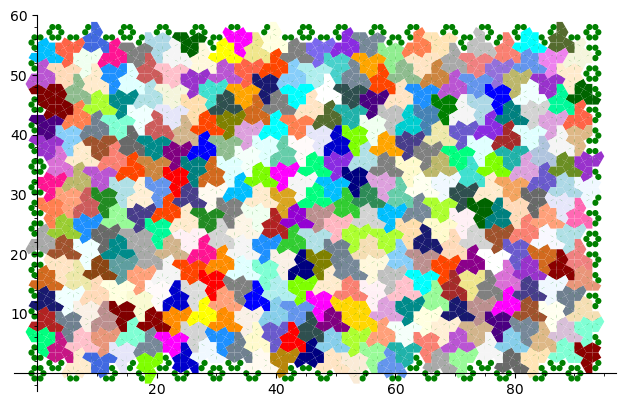
Dans la manière de résoudre la question ci-haut, le problème est représenté par un problème de couverture exacte qui consiste à recouvrir exactement les entiers de 1 à n avec des sous-ensembles choisis dans une liste de sous-ensembles déterminés. Ici, on représente l'espace à recouvrir de manière discrète en comptant 6 points du plan par hexagone (un point pour chaque kite contenu dans un hexagone). Rappelons que la pièce Chapeau qui nous intéresse est formée d'une union d'exactement 8 de ces kites.
sage: s.plot_domain()

Ensuite, on construit une matrice de 0 et de 1 avec autant de colonnes que de points ci-haut (16 * 17 * 2 * 6 = 3264) et autant de lignes qu'il y a de copies isométriques de la pièce intersectant le domaine. Pour chaque copie de la pièce, une ligne dans la matrice contient des 1 exactement dans les colonnes associées aux kites occupés par la pièce.
sage: s.the_dlx_solver() Dancing links solver for 3264 columns and 7116 rows
Le calcul ci-haut qui a construit la matrice (sparse) indique qu'il y a 7116 copies isométriques de la pièce qui intersectent (complètement ou partiellement) le domaine. Quand on voudra dessiner une solution, on ignorera les pièces incomplètes.
On peut maintenant résoudre le problème.
sage: s = MonotileSolver(8,8) sage: %time L = s.one_solution() # l'algo des liens dansants de Knuth est utilisé par défaut CPU times: user 798 ms, sys: 32.2 ms, total: 830 ms Wall time: 1min 20s
Le contenu d'une solution est une liste de nombres indiquant les lignes de la matrice de 0/1 à considérer pour former une solution. C'est-à-dire que la sous-matrice restreinte aux lignes données comporte exactement un 1 dans chaque colonne:
sage: L [81, 85, 125, 128, ... 1772, 1783, 1794, 1815]
Ici, il se trouve que les solveurs SAT sont plus efficaces que l'algo des liens dansants pour trouver une solution:
sage: %time L = s.one_solution(solver='glucose') CPU times: user 326 ms, sys: 16.1 ms, total: 342 ms Wall time: 526 ms sage: %time L = s.one_solution(solver='kissat') CPU times: user 335 ms, sys: 3.64 ms, total: 339 ms Wall time: 461 ms
En effet, Glucose se comporte plutôt bien pour résoudre des problèmes de pavages du plan lorsqu'il existe une solution. Mais lorsqu'il n'y a pas de solution, l'algo des liens dansants de Knuth est parfois mieux. Aussi, l'algo des liens dansants de Knuth est très efficace pour énumérer toutes les solutions.
Le solveur Kissat a été ajouté dans SageMath par moi-même comme package optionnel cette année suite à une discussion avec Laurent Simon au café du LaBRI. On peut installer le solveur kissat dans SageMath avec la commande sage -i kissat.
Ici on extrait le contour des pièces d'une solution (tel que chaque arête est dessinée une seule fois afin d'éviter que la découpeuse laser passe deux fois par chaque arête ce qui peut endommager ou brûler le bord des pièces en bois) et on crée un fichier pdf ou svg. Je choisis une taille de 16 double-hexagones horizontalement et 17 verticalement, car cela crée un fichier qui correspond à une taille de 1m x 60cm. C'est la taille de la découpeuse laser à notre disposition:
sage: s = MonotileSolver(16, 17) sage: tikz = s.one_solution_tikz(solver='glucose') sage: tikz.pdf('solution_16x17.pdf') sage: tikz.svg('solution_16x17.svg') # or
Avec l'aide de David Renault, mon collègue du LaBRI qui enseigne à l'ENSEIRB et qui m'a déjà accompagné dans la réalisation de projets de découpe laser, nous avons découpé le fichier ci-haut le jeudi 27 avril au EirLab, l'atelier de fabrication numérique (FabLab) de l'ENSEIRB-MATMECA:
Comme toujours, il faut quelque peu modifier le fichier svg dans Inkscape avant de lancer la découpe laser. Voici le fichier modifié juste avant la découpe.
Maintenant, on peut s'amuser avec les pièces:
Avec mes garçons, nous avons trouvé une forme intéressante qui recouvre le plan périodiquement à l'exception d'un trou hexagonal. Il se trouve que la même forme peut-être créée de deux façons différentes: sur l'image ci-bas la forme à droite est la globalement la même, mais elle n'est pas obtenue de la même façon que celle en haut à gauche. Pourtant, toutes deux ont le même contour extérieur et le même trou hexagonal.
Cette observation, déjà faite par d'autres, a mené au recouvrement d'une sphère avec la pièce et un trou pentagonal:

Next Page »
