Are losers more spirited in ultimate? a data analysis based on 1500 games played during WMUCC, WUCC and CUC 2022
17 octobre 2022 | Mise à jour: 24 octobre 2022 | Catégories: python, ultimate | View CommentsUPDATE (Oct 24, 2022), thanks to comments from reddit: fixed the way standard deviation is presented to avoid misinterpretation, removed the sin(-x) graphics.
When I started to play ultimate in September 2002 in Sherbrooke, the local team Stakatak was just coming back their very first (or maybe second?) participation at the Canadian Ultimate Championship, in the mixed division. I remember they lost all of their nine games and finished 16th out of 16 teams. But they came back in Sherbrooke with the "Spirit of the Game" award which we were very proud of.
What I want to discuss here is not whether the team that lose all its games and wins the Spirit of the Game deserves it or not. The question I want to consider in this blog post is about the evaluation of the spirit of the game in a typical ultimate frisbee game: are we biased by the end result of the game (win vs lose) when we evaluate the opponent's spirit of the game? In particular:
- do we give more spirit points to the opponent team when the opponent has lost against us?
- do we give less spirit points to the opponent team when the opponent has won against us?
The Spirit of the Game
As not everyone reading this post ever played an ultimate frisbee game, let me recall what is the spirit of the game and how it is evaluated nowadays in a tournament. As Ultimate (frisbee) is a self-officiated team sport, the spirit of the game is important. Every team thinks they have a good spirit but not every opponent agree. There are ways for teams to help (or force) them improve their spirit of the game, the most important one being the end of game discussion during which the two teams discuss the game and if necessary any issues that happenned during the game. Another is the evaluation of the spirit of the game by the opponent team, which is made by evaluating 5 subjects:
- Rules Knowledge and Use (4 points)
- Fouls and Body Contact (4 points)
- Fair-Mindedness (4 points)
- Positive Attitude and Self-Control (4 points)
- Communication (4 points)
In Ultimate tournaments, the spirit scores of each team is public and allows to evaluate and rank each team. When a team is low ranked, it shows without ambiguity that the community thinks this team needs to improve because it was badly evaluated by more than one team. This peer-pressure contributes to make teams improve themselve. The ranking is also used to elect a most spirited team which is often given a "Spirit of the game" trophee at the end of the tournament.
Three tournaments considered for the data analysis
For the data analysis, we consider the following three tournaments that were held during Summer 2022:
- World Masters Ultimate Club Championships (WMUCC) 2022, Limerick, Ireland, June 25th to July 2nd 2022
- World Ultimate Club Championships (WUCC) 2022, Cincinnati Ohio, USA, July 23-30, 2022
- Canadian Ultimate Championships (CUC) 2022, Brampton, Ontario, August 18-21, 2022
These tournaments all use the Ultiorganizer website which allows to parse the results with the same Python script which I have made public.
In total, 1540 games were played in these 3 tournaments. Unfortunately, the score or the spirit score was not completed or is not available for all games. Maybe because teams forgot to provide the spirit scores or maybe the game was not played at all. We were able to access all needed data including final score and spirit scores for 1448 of the games (94 %). Since the spirit of both teams gets evaluated during a game, this means 1448 x 2 = 2896 evaluations of a team spirit.
| Tournament | Number of games | Number of games with complete data |
|---|---|---|
| WMUCC 2022 | 589 | 548 (93 %) |
| WUCC 2022 | 652 | 628 (96 %) |
| CUC 2022 | 299 | 272 (91 %) |
| Total | 1540 | 1448 (94 %) |
Average Spirit Points
The average spirit points received by a team is shown in the table below for each of the three considered tournaments.
| Tournament | mean | std |
|---|---|---|
| WMUCC 2022 | 11.307 | 1.830 |
| WUCC 2022 | 10.561 | 1.685 |
| CUC2022 | 10.821 | 2.009 |
Spirit points are on average slightly above 10. Also, at WMUCC, the spirit points were higher in general, slightly above 11. We may interpret this as the fact that older master players playing for a long time were happy to play again at the international level after the pandemia and meet old friends which contributed to have nice spirited games in Limerick (why did not I try to go at Limerick again? I miss my old friends from Epoq or Nsom or Quarantine!).
Average Spirit Points for losers/winners
Now let's compare the average spirit points given to the loser of a game vs to the winner of a game. In the three considered tournaments, on average it turns out that the loser of the game always gets more spirit points. See the results in the following table.
| Tournament | When winning (mean; std) | When losing (mean; std) |
|---|---|---|
| WMUCC 2022 | 10.904; 1.756 | 11.709; 1.815 |
| WUCC 2022 | 10.323; 1.707 | 10.800; 1.630 |
| CUC2022 | 10.566; 2.101 | 11.076; 1.882 |
We visualize below the distribution of spirit scores at WMUCC 2022 for losers vs winners with the following box plot graphics made with matplotlib through the pandas library. Small circle indicate what is called flier points. As mentionned in the matplotlib boxplot documentation, "flier points are those past the end of the whiskers".
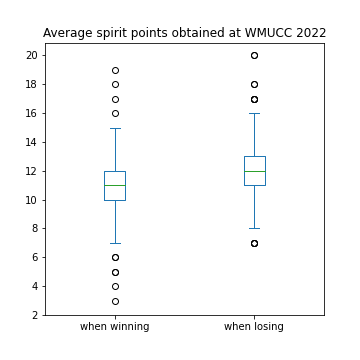
Are losers more spirited in ultimate?
We can now answer the question asked in the title of this blog post and the answer is yes: the data says that losers are more spirited in Ultimate.
Or, alternatively, we can assume the hypothesis that losers and winners are equally spirited. This assumption implies that players must be biased by the end result of the game when evaluating the opponent's spirit of the game.
Lose-win Bias
It is natural to define the lose-win bias as the difference between the average spirit points obtained by the losing team and the winning team. In other words, how much more spirited are losers than winners? The results is in the following table.
| Tournament | lose-win bias |
|---|---|
| WMUCC 2022 | 0.8043 |
| WUCC 2022 | 0.4768 |
| CUC2022 | 0.5101 |
At WUCC 2022 and CUC 2022, the losing team gets approximatively 0.5 more spirit points than the winning team. During WMUCC 2022, the losing team was obtaining 0.8 more spirit points than the winning team.
Interpretation
How can we interpret these results? Are losers really more spirited or can we accept that we are biased? Is there any other way to interpret the above results?
My interpretation is that we are biased by the end result which means winners and losers will say something like this (if I allow myself to caricature in a provocative way):
"Dear opponent, thanks for losing, we will give you one more spirit point for not making more effort."
"Dear opponent, thanks for the game, you won against us, but your communication was not so good, we give you one point less than we would have usually gave if you would have accepted to lose the game."
Of course I am volontarily exagerating and being a little provocative here to make us think about our own biases. We would never say sentences like this, but, basicaly, I think we might be actually doing this sometimes in a more disguised way.
I think that it is necessary that every ultimate frisbee player know about the existence of this lose-win bias in order to become more objective when evaluating the spirit of the game of the opponent.
Spirit score per score differential
I suggest now to go a bit further in the data analysis. Instead of splitting the spirit points according to the two win or lose cases, we can study the spirit points according to the score differential. This should allow us to answer interesting questions such as:
- Is winning by 1 point the worse thing to do to get a good spirit?
- By how many points should a team win to expect the most spirit points?
- By how many points should a team win to leverage the spirit bias?
Below is a graphics which shows the average spirit point obtained by a team according to the point differential during the three considered tournaments:
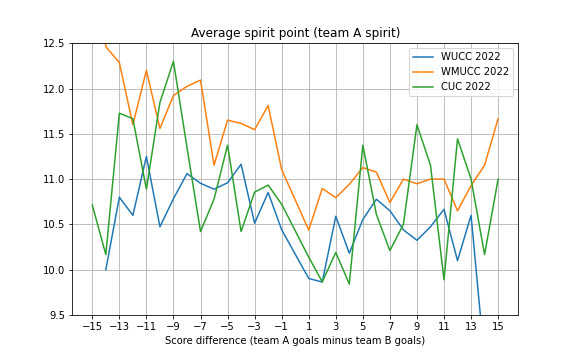
We observe that spirit scores were in general higher at WMUCC 2022. Also, we can see that each curve reach its minimum around +1 or +2, which means you want to win by more than one or two points if you want to win and maximize your spirit points.
Bias per score differential
In what follows, we will discuss the bias per score differential. Here is the graphics summarizing the average lose-win bias according to the end of game point differential (one broken line per tournament):
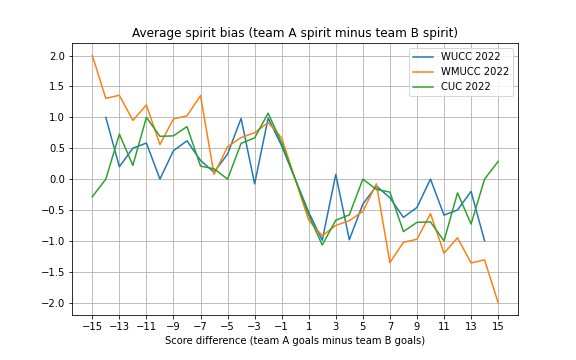
Let's first try to explain the above graphics. The x-axis shows by how much you won the game: +2 means you won the game by 2, and -5 means you lost the game by 5. The graphics shows for each score difference, the average difference between your team spirit score and the opponent spirit score for each of the three tournaments. Take for example the case when your team win by 2, the graphics shows that on average in all of the three tournaments, the spirit score you get is 1 less than the losing team.
Some similarities appear in the three tournaments. On the right part of the graphics, for positive values on the x-axis, the graphic lines are below zero whereas for negative values on the x-axis, the graphic lines are above zero. This essentially means that losers have on average a better spirit evaluation than winners.
One could have expected that winning by one point is worse than winning by two points, because it is in this kind of game that a single action where a travel or fault is called that may affect the outcome of the game, thus affecting the spirit results. But the data shows that winning by 2 is worse than winning by 1 in terms of spirit bias. A possible interpretation goes as follows. When you lose on the universe point, you show to everyone that you were very close to win which is a honorific way of losing. On the other hand, losing by 2 does not allow you to pretend you were close enough to win the game. This may explain why the spirit bias is higher for game finishing by a difference of 2 points compared to 1 point.
Another pattern which is common in each of the three lines is that a local minimum for the lose-win bias is reached when winning by 2. It seems that winning by a higher margin (3, 4, 5 or 6 points) makes the lose-win bias globally closer to zero.
My personnal interpretation is as follows. Winning by 1 or 2 points is not good for your spirit points, because you basically allow your opponent to think that they could have won the game (which may make them biased when evaluating your spirit points). Winning by 5 or 6 points seems to neutralize the win-lose bias. This is enough a point difference which establishes a hierarchy and makes the opponent accept their lost, but not too much that part of the game become meaningless which may impact the fun of both team to play the game.
When the score difference increases, what happens is more chaotic, so I don't know if we can make any safe interpretations, but it seems winning by 7, 8 or 9 is not good for your spirit. And then, winning by exactly 10 points seems also to neutralize the bias. There are fewer games finishing by a difference of more than 10 points, so I will not discuss their statistics here.
Conclusion
To conclude, I would like to recall the real objective of this blog post which is to make the ultimate frisbee players acknowledge the existence of biases when evaluating the opponent's spirit of game, one bias being related to the score result outcome. Once this is acknowledged, the next step is to search for ways to leverage the bias. This task belongs to each and every ultimate frisbee players.
Code and data
I made my code public allows to reproduce the computations and graphics. Everything is in this gitlab repository:
https://gitlab.com/seblabbe/spirit-bias-in-ultimate
The code is written in Python. Data is downloaded with urllib library and stored as csv files. Parsing of Ultiorganizer websites is done in a Python script ultiorganizer_parser.py that I wrote. Analysis of the csv files is done with pandas library with Jupyter notebooks. Graphics are made with matplotlib.
À Liège, une piste cyclable dans la trémie parking du pont Kennedy
20 juin 2022 | Catégories: urbanisme | View CommentsJeudi 16 juin 2022, en marchant du centre vers le parc de la Boverie pour le rendez-vous du jeudi soir de la conférence DYADISC, j'ai eu l'agréable surprise de voir que trois des 25 suggestions que j'avais faites en 2016 ont été réalisées:
- Créer une piste cyclable dans la trémie parking du pont Kennedy, afin de désengorger la ravel qui devrait être réservée aux piétons qui marchent le long de la meuse.
- Sur le quai Marcellis, remplacer du stationnement par une piste cyclable qui emprunte la trémie du pont Kennedy, pour la même raison de réserver le ravel aux piétons dans Outremeuse.
- Créer une piste cyclable sur la place Cockerill pour prolonger le flux de vélo qui emprunte la passerelle piétonne devant la Grande Poste.
C'est super!
Using Glucose SAT solver to find a tiling of a rectangle by polyominoes
27 mai 2021 | Mise à jour: 20 juin 2022 | Catégories: sage, math | View CommentsIn his Dancing links article, Donald Knuth considered the problem of packing 45 Y pentaminoes into a 15 x 15 square. We can redo this computation in SageMath using some implementation of his dancing links algorithm.
Dancing links takes 1.24 seconds to find a solution:
sage: from sage.combinat.tiling import Polyomino, TilingSolver sage: y = Polyomino([(0,0),(1,0),(2,0),(3,0),(2,1)]) sage: T = TilingSolver([y], box=(15, 15), reusable=True, reflection=True) sage: %time solution = next(T.solve()) CPU times: user 1.23 s, sys: 11.9 ms, total: 1.24 s Wall time: 1.24 s
The first solution found is:
sage: sum(T.row_to_polyomino(row_number).show2d() for row_number in solution)

What is nice about dancing links algorithm is that it can list all solutions to a problem. For example, it takes less than 3 minutes to find all solutions of tiling a 15 x 15 rectangle with the Y polyomino:
sage: %time T.number_of_solutions() CPU times: user 2min 46s, sys: 3.46 ms, total: 2min 46s Wall time: 2min 46s 1696
It takes more time (38s) to find a first solution of a larger 20 x 20 rectangle:
sage: T = TilingSolver([y], box=(20,20), reusable=True, reflection=True) sage: %time solution = next(T.solve()) CPU times: user 38.2 s, sys: 7.88 ms, total: 38.2 s Wall time: 38.2 s
The polyomino tiling problem is reduced to an instance of the universal cover problem which is represented by a sparse matrix of 0 and 1:
sage: dlx = T.dlx_solver() sage: dlx Dancing links solver for 400 columns and 2584 rows
We observe that finding a solution to this problem takes the same amount of time. This is normal since it is exactly what is used behind the scene when calling next(T.solve()) above:
sage: %time sol = dlx.one_solution(ncpus=1) CPU times: user 38.6 s, sys: 48 ms, total: 38.6 s Wall time: 38.5 s
One way to improve the time it takes it to split the problem into parts and use many processors to work on each subproblems. Here a random column is used to split the problem which may affect the time it takes. Sometimes a good column is chosen and it works great as below, but sometimes it does not:
sage: %time sol = dlx.one_solution(ncpus=2) CPU times: user 941 µs, sys: 32 ms, total: 32.9 ms Wall time: 1.41 s
The reduction from dancing links instance to SAT instance #29338 and to MILP instance #29955 was merged into SageMath 9.2 during the last year. A discussion with Franco Saliola motivated me to implement these translations since he was also searching for faster way to solve dancing links problems. Indeed some problems are solved faster with other kind of solver, so it is good to make some comparisons between solvers.
Therefore, with a recent enough version of SageMath, we can now try to find a tiling with other kinds of solvers. Following my experience with tilings by Wang tiles, I know that Glucose SAT solver is quite efficient to solve tilings of the plane. This is why I test this one below. Glucose is now an optional package to SageMath which can be installed with:
sage -i glucose
Update (June 20th, 2022): It seems sage -i glucose no longer works. The new procedure is to use ./configure --enable-glucose when installation is made from source. See the question Unable to install glucose SAT solver with Sage on ask.sagemath.org for more information.
Glucose finds the solution of a 20 x 20 rectangle in 1.5 seconds:
sage: %time sol = dlx.one_solution_using_sat_solver('glucose') CPU times: user 306 ms, sys: 12.1 ms, total: 319 ms Wall time: 1.51 s
The rows of the solution found by Glucose are:
sage: sol [0, 15, 19, 38, 74, 245, 270, 310, 320, 327, 332, 366, 419, 557, 582, 613, 660, 665, 686, 699, 707, 760, 772, 774, 781, 802, 814, 816, 847, 855, 876, 905, 1025, 1070, 1081, 1092, 1148, 1165, 1249, 1273, 1283, 1299, 1354, 1516, 1549, 1599, 1609, 1627, 1633, 1650, 1717, 1728, 1739, 1773, 1795, 1891, 1908, 1918, 1995, 2004, 2016, 2029, 2037, 2090, 2102, 2104, 2111, 2132, 2144, 2146, 2185, 2235, 2301, 2460, 2472, 2498, 2538, 2548, 2573, 2583]
Each row correspond to a Y polyomino embedded in the plane in a certain position:
sage: sum(T.row_to_polyomino(row_number).show2d() for row_number in sol)

Glucose-Syrup (a parallelized version of Glucose) takes about the same time (1 second) to find a tiling of a 20 x 20 rectangle:
sage: T = TilingSolver([y], box=(20, 20), reusable=True, reflection=True) sage: dlx = T.dlx_solver() sage: dlx Dancing links solver for 400 columns and 2584 rows sage: %time sol = dlx.one_solution_using_sat_solver('glucose-syrup') CPU times: user 285 ms, sys: 20 ms, total: 305 ms Wall time: 1.09 s
Searching for a tiling of a 30 x 30 rectangle, Glucose takes 40s and Glucose-Syrup takes 16s while dancing links algorithm takes much longer (next(T.solve()) which is using dancing links algorithm does not halt in less than 5 minutes):
sage: T = TilingSolver([y], box=(30,30), reusable=True, reflection=True) sage: dlx = T.dlx_solver() sage: dlx Dancing links solver for 900 columns and 6264 rows sage: %time sol = dlx.one_solution_using_sat_solver('glucose') CPU times: user 708 ms, sys: 36 ms, total: 744 ms Wall time: 40.5 s sage: %time sol = dlx.one_solution_using_sat_solver('glucose-syrup') CPU times: user 754 ms, sys: 39.1 ms, total: 793 ms Wall time: 16.1 s
Searching for a tiling of a 35 x 35 rectangle, Glucose takes 2min 5s and Glucose-Syrup takes 1min 16s:
sage: T = TilingSolver([y], box=(35, 35), reusable=True, reflection=True) sage: dlx = T.dlx_solver() sage: dlx Dancing links solver for 1225 columns and 8704 rows sage: %time sol = dlx.one_solution_using_sat_solver('glucose') CPU times: user 1.07 s, sys: 47.9 ms, total: 1.12 s Wall time: 2min 5s sage: %time sol = dlx.one_solution_using_sat_solver('glucose-syrup') CPU times: user 1.06 s, sys: 24 ms, total: 1.09 s Wall time: 1min 16s
Here are the info of the computer used for the above timings (a 4 years old laptop runing Ubuntu 20.04):
$ lscpu Architecture : x86_64 Mode(s) opératoire(s) des processeurs : 32-bit, 64-bit Boutisme : Little Endian Address size : 39 bits physical, 48 bits virtual Processeur(s) : 8 Liste de processeur(s) en ligne : 0-7 Thread(s) par coeur : 2 Coeur(s) par socket : 4 Socket(s) : 1 Noeud(s) NUMA : 1 Identifiant constructeur : GenuineIntel Famille de processeur : 6 Modèle : 158 Nom de modèle : Intel(R) Core(TM) i7-7820HQ CPU @ 2.90GHz Révision : 9 Vitesse du processeur en MHz : 3549.025 Vitesse maximale du processeur en MHz : 3900,0000 Vitesse minimale du processeur en MHz : 800,0000 BogoMIPS : 5799.77 Virtualisation : VT-x Cache L1d : 128 KiB Cache L1i : 128 KiB Cache L2 : 1 MiB Cache L3 : 8 MiB Noeud NUMA 0 de processeur(s) : 0-7
To finish, I should mention that the implementation of dancing links made in SageMath is not the best one. Indeed, according to what Franco Saliola told me, the dancing links code written by Donald Knuth himself and available on his website (franco added some makefile to compile it more easily) is faster. It would be interesting to confirm this and if possible improves the implementation made in SageMath.
Installation de Python, Jupyter et JupyterLab
23 février 2021 | Catégories: sage, math | View CommentsL'École doctorale de mathématiques et informatique (EDMI) de l'Université de Bordeaux offre des cours chaque année. Dans ce cadre, cette année, je donnerai le cours Calcul et programmation avec Python ou SageMath et meilleures pratiques qui aura lieu les 25 février, 4 mars, 11 mars, 18 mars 2021 de 9h à 12h.
Le créneau du jeudi matin correspond au créneau des Jeudis Sage au LaBRI où un groupe d'utilisateurs de Python se rencontrent toutes les semaines pour faire du développement tout en posant des questions aux autres utilisateurs présents.
Le cours aura lieu sur le logiciel BigBlueButton auquel les participantEs inscritEs se connecteront par leur navigateur web (Mozilla Firefox ou Google Chrome). Selon les exigences minimales du client BigBlueButton, il faut éviter Safari ou IE, sinon certaines fonctionnalités ne marchent pas. Vous pouvez vous familiariser avec l'interface BigBlueButton en écoutant ce tutoriel BigBlueButton (sur youtube, 5 minutes). Consultez les pages de support suivantes en cas de soucis audio ou internet.
Pour la première séance, nous présenterons les bases de Python et les différentes interfaces. Nous ne pourrons pas passer trop de temps à faire l'installation des différents logiciels. Il serait donc préférable si les installations ont déjà été faites avant le cours par chacun des participantEs. Cela vous permettra de reproduire les commandes montrées et faire des exercices.
Les logiciels à installer avant le cours sont:
- Python3
- SageMath (facultatif)
- IPython
- Jupyter notebook classique
- JupyterLab
Python 3: Normalement, Python est déjà installé sur votre ordinateur. Vous pouvez le confirmer en tapant python ou python3 dans un terminal (Linux/Mac) ou dans l'invité de commande (Windows). Vous devriez obtenir quelque chose qui ressemble à ceci:
Python 3.8.5 (default, Jul 28 2020, 12:59:40) [GCC 9.3.0] on linux Type "help", "copyright", "credits" or "license" for more information. >>>
SageMath (facultatif): SageMath est un logiciel libre de mathématiques basé sur Python et regroupant des centaines de packages et librairies. Il y a plusieurs manières d'installer SageMath, et je vous recommande de lire cette documentation pour déterminer la manière de l'installer qui vous convient le mieux. Sinon, vous pouvez télécharger directement les binaires ici.
Vous devriez obtenir quelque chose qui ressemble à ceci:
┌────────────────────────────────────────────────────────────────────┐ │ SageMath version 9.2, Release Date: 2020-10-24 │ │ Using Python 3.8.5. Type "help()" for help. │ └────────────────────────────────────────────────────────────────────┘ sage:
IPython:
Si vous avez déjà installé SageMath, c'est bon, car ipython en fait partie. La commande sage -ipython vous permettra de l'ouvrir.
Si vous n'avez pas SageMath, vous pouvez l'installer via pip install ipython ou sinon en suivant ces instructions du site ipython. Ensuite, la commande ipython dans le terminal (Linux, OS X) ou dans l'invité de commande (Windows) vous permettra de l'ouvrir.
Vous devriez obtenir quelque chose qui ressemble à ceci:
Python 3.8.5 (default, Jul 28 2020, 12:59:40) Type 'copyright', 'credits' or 'license' for more information IPython 7.13.0 -- An enhanced Interactive Python. Type '?' for help. In [1]:
Jupyter:
Si vous avez déjà installé SageMath, c'est bon, car Jupyter en fait partie. La commande sage -n jupyter vous permettra de l'ouvrir.
Si vous n'avez pas SageMath, vous pouvez suivre ces instructions du site jupyter.org. Ensuite, la commande jupyter notebook dans le terminal (Linux, OS X) ou dans l'invité de commande (Windows) vous permettra de l'ouvrir.
Vous devriez obtenir quelque chose qui ressemble à ceci dans votre navigateur:
JupyterLab:
Si vous avez déjà installé SageMath, vous pouvez installer JupyterLab en faisant sage -i jupyterlab et l'ouvrir en faisant sage -n jupyterlab. Sur Windows, c'est un tout petit peut différent, il faut plutôt faire pip install jupyterlab dans la console SageMath selon cette récente réponse sur ask.sagemath.org.
Si vous n'avez pas SageMath, vous pouvez suivre les instructions du même site que ci-haut. Ensuite, la commande jupyter-lab ou jupyter lab dans le terminal (Linux, OS X) ou dans l'invité de commande (Windows) vous permettra de l'ouvrir.
Vous devriez obtenir quelque chose qui ressemble à ceci dans votre navigateur:
Tiling a polyomino with polyominoes in SageMath
03 décembre 2020 | Catégories: sage, math | View CommentsSuppose that you 3D print many copies of the following 3D hexo-mino at home:
sage: from sage.combinat.tiling import Polyomino, TilingSolver sage: p = Polyomino([(0,0,0), (0,1,0), (1,0,0), (2,0,0), (2,1,0), (2,1,1)], color='blue') sage: p.show3d() Launched html viewer for Graphics3d Object

You would like to know if you can tile a larger polyomino or in particular a rectangular box with many copies of it. The TilingSolver module in SageMath is made for that. See also this recent question on ask.sagemath.org.
sage: T = TilingSolver([p], (7,5,3), rotation=True, reflection=False, reusable=True) sage: T Tiling solver of 1 pieces into a box of size 24 Rotation allowed: True Reflection allowed: False Reusing pieces allowed: True
There is no solution when tiling a box of shape 7x5x3 with this polyomino:
sage: T.number_of_solutions() 0
But there are 4 solutions when tiling a box of shape 4x3x2 with this polyomino:
sage: T = TilingSolver([p], (4,3,2), rotation=True, reflection=False, reusable=True) sage: T.number_of_solutions() 4
We construct the list of solutions:
sage: solutions = [sol for sol in T.solve()]
Each solution contains the isometric copies of the polyominoes tiling the box:
sage: solutions[0] [Polyomino: [(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 1, 0), (2, 0, 0), (2, 1, 0)], Color: #ff0000, Polyomino: [(0, 1, 1), (0, 2, 0), (0, 2, 1), (1, 1, 1), (2, 1, 1), (2, 2, 1)], Color: #ff0000, Polyomino: [(1, 0, 0), (1, 0, 1), (2, 0, 1), (3, 0, 0), (3, 0, 1), (3, 1, 0)], Color: #ff0000, Polyomino: [(1, 2, 0), (1, 2, 1), (2, 2, 0), (3, 1, 1), (3, 2, 0), (3, 2, 1)], Color: #ff0000]
It may be easier to visualize the solutions, so we define the following function allowing to draw the solutions with different colors for each piece:
sage: def draw_solution(solution, size=0.9): ....: colors = rainbow(len(solution)) ....: for piece,col in zip(solution, colors): ....: piece.color(col) ....: return sum((piece.show3d(size=size) for piece in solution), Graphics())
sage: G = [draw_solution(sol) for sol in solutions] sage: G [Graphics3d Object, Graphics3d Object, Graphics3d Object, Graphics3d Object]
sage: G[0] # in Sage, this will open a 3d viewer automatically
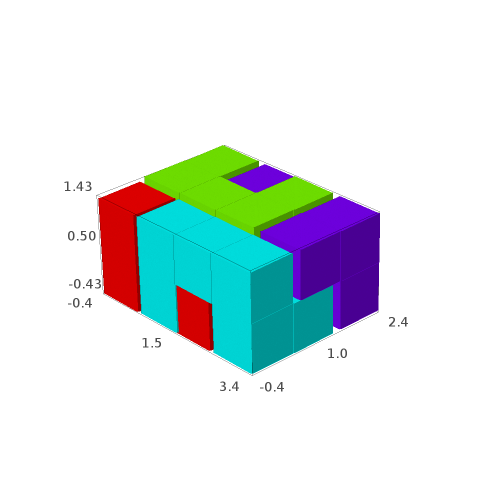
sage: G[1]
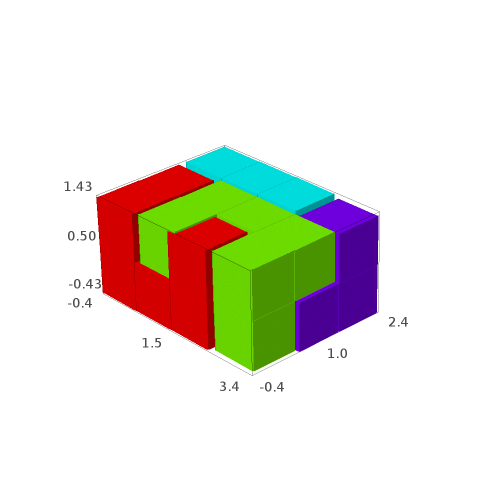
sage: G[2]

sage: G[3]
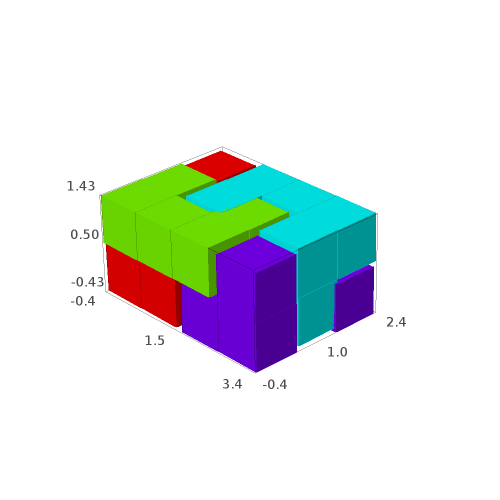
We may save the solutions to a file:
sage: G[0].save('solution0.png', aspect_ratio=1, zoom=1.2) sage: G[1].save('solution1.png', aspect_ratio=1, zoom=1.2) sage: G[2].save('solution2.png', aspect_ratio=1, zoom=1.2) sage: G[3].save('solution3.png', aspect_ratio=1, zoom=1.2)
Question: are all of the 4 solutions isometric to each other?
The tiling problem is solved due to a reduction to the exact cover problem for which dancing links Knuth's algorithm provides all the solutions. One can see the rows of the dancing links matrix as follows:
sage: d = T.dlx_solver() sage: d Dancing links solver for 24 columns and 56 rows sage: d.rows() [[0, 1, 2, 4, 5, 11], [6, 7, 8, 10, 11, 17], [12, 13, 14, 16, 17, 23], ... [4, 6, 7, 9, 10, 11], [10, 12, 13, 15, 16, 17], [16, 18, 19, 21, 22, 23]]
The solutions to the dlx solver can be obtained as follows:
sage: it = d.solutions_iterator() sage: next(it) [3, 36, 19, 52]
These are the indices of the rows each corresponding to an isometric copy of the polyomino within the box.
Since SageMath-9.2, the possibility to reduce the problem to a MILP problem or a SAT instance was added to SageMath (see #29338 and #29955):
sage: d.to_milp() (Boolean Program (no objective, 56 variables, 24 constraints), MIPVariable of dimension 1) sage: d.to_sat_solver() CryptoMiniSat solver: 56 variables, 2348 clauses.
« Previous Page -- Next Page »
