WeBWorK, un logiciel pour les devoirs en ligne
04 janvier 2012 | Catégories: webwork | View CommentsJ'ai appris l'existence de WeBWorK lors des Sage Days 31 à Seattle en juin 2011, où j'ai rencontré Jason Aubray et Michael Gage, deux leaders de ce projet. Leur projet pour la semaine était d'intégrer Sage à WeBWorK et d'intégrer WeBWorK à Sage.
WeBWorK est un logiciel libre qui permet aux étudiants de faire des devoirs de mathématiques et de sciences en ligne. WeBWorK est soutenu par la Mathematical Association of America et la National Science Foundation et est livré avec une bibliothèque de plus de 20000 exercices. Les cours pris en charge incluent l'algèbre du collège, les mathématiques discrètes, probabilités et statistiques, calcul simple et multivariée, les équations différentielles, algèbre linéaire et l'analyse complexe.
WeBWorK au Québec
WeBWorK est utilisé au Québec dans certaines écoles anglophones depuis quelques années déjà. Alice McLeod, enseignante au Cégep John Abbott College, l'utilise dans des cours de mathématiques. On peut lire sur son expérience dans le texte Les mathématiques et les TIC, des virus qui s’attrapent... paru sur Profweb en 2009. Rhys Adams, enseignant au Cégep Vanier College, l'utilise dans des cours de physique. On peut lire sur son expérience dans le texte Using Webwork to Enliven Discussion in Physics Classrooms aussi paru sur Profweb en 2010.
WeBWorK à l'UQAM via Moodle
À l'automne 2011, je donnais le cours de MAT1112 Calcul I à l'Université du Québec à Montréal. J'en ai profité pour tester l'outil WeBWorK et de l'utiliser pour une des premières fois dans le monde dans un cours en français.
Pour ce faire, j'aurais pu profiter de la Mathematical Association of America qui offre gratuitement l'utilisation de son serveur pour au plus un cours par université contenant au plus 100 étudiants. Mais, on a plutôt opté pour une configuration locale.
Grâce à l'équipe Moodle de l'UQAM et en particulier Stéphanie Lanthier, je n'ai pas eu à m'occuper de plusieurs aspects techniques : installation de WeBWorK, configuration du serveur WeBWorK, configuration de la passerelle entre le serveur WeBWorK et Moodle. À la mi-septembre, le tout était configuré. Pour plus d'informations, visitez la page Guide d'installation de WeBWork 2.5 sur CentOS 5 écrite par Stéphanie et la page Moodle Integration toutes deux disponibles sur le wiki de WeBWork.
L'utilisation de WeBWorK via Moodle a l'avantage de gérer les comptes étudiants automatiquement. C'est Moodle qui s'en occupe. Cela permet aux étudiants de faire les exercices WeBWorK directement dans leur compte Moodle, site qu'ils consultent déjà régulièrement.
Avec Stéphanie, nous avons aussi traduit (bénévolement) l'interface WeBWorK en français. À ce jour, nous n'avons toujours pas terminé cette traduction, car nous nous sommes concentrés sur la traduction de l'interface vue par l'étudiant. Mais, on a fait au moins la moitié et nous comptons terminer bientôt. La traduction sera disponible dans la version officielle de WeBWorK.
Ensuite, tout ce qu'il me restait à faire en tant que chargé de cours était de choisir (et traduire) des problèmes. Durant l'automne 2011, j'ai traduit une dizaine de questions par semaine. Ceux-ci seront disponibles à l'avenir pour les personnes qui enseigneront le même cours.
Ci-bas, voici quelques images qui illustrent l'interface et qui donnent un aperçu de son utilisation.
Un problème en anglais:
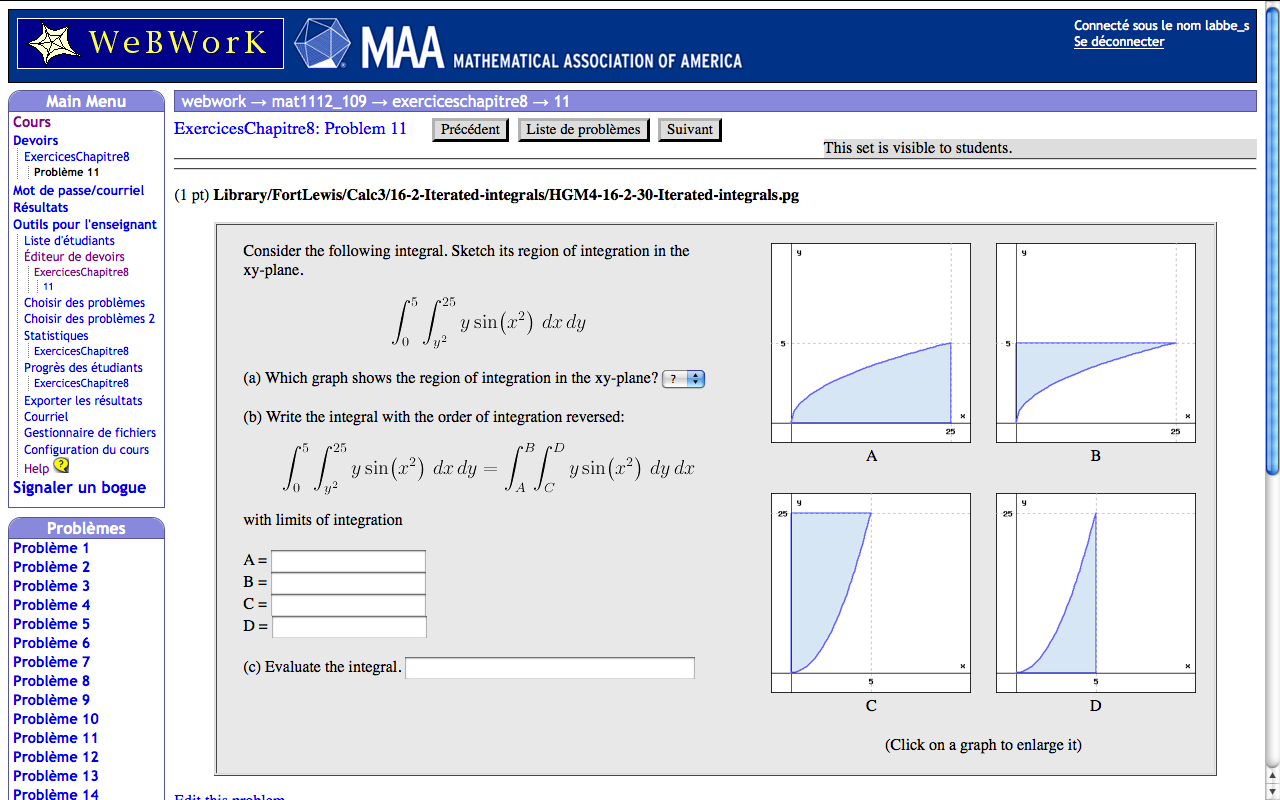
Le même problème que j'ai traduit en français:
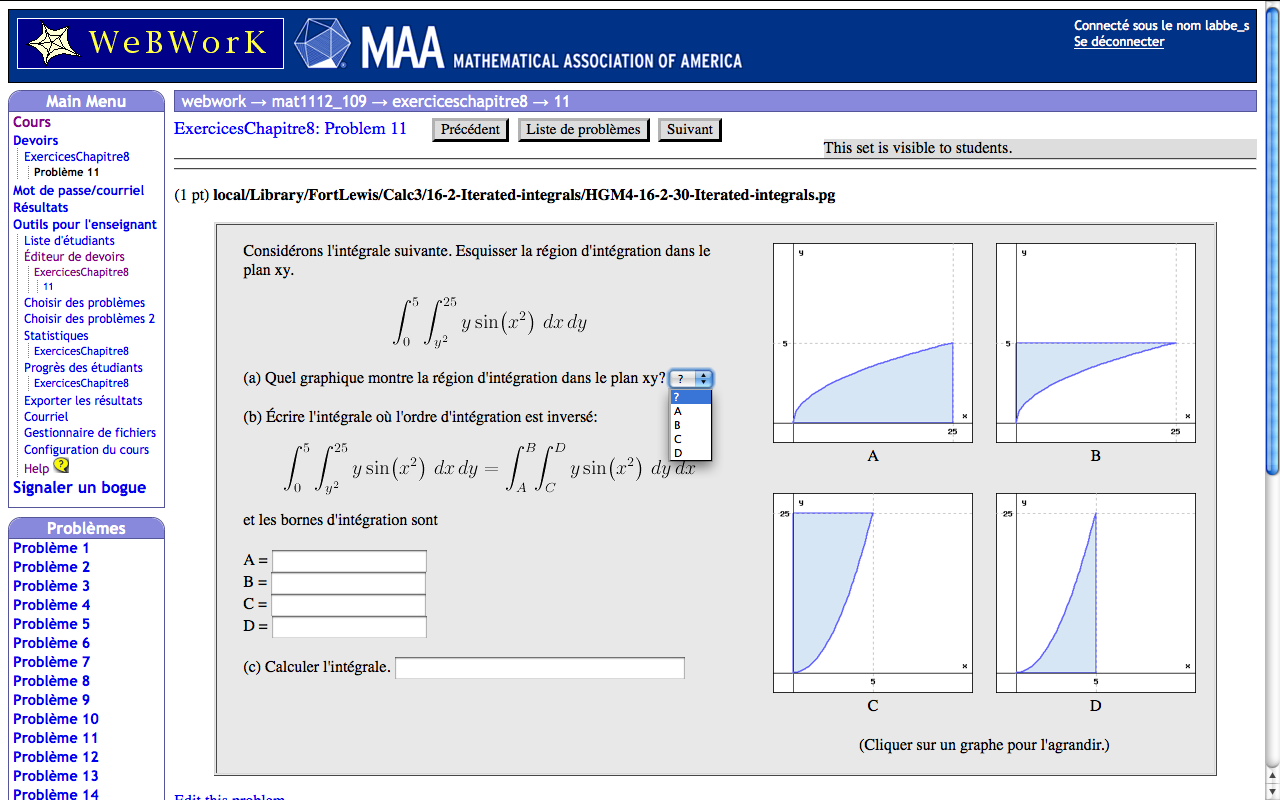
Le même problème vu par un autre utilisateur:
Les paramètres sont choisis aléatoirement de sorte que les étudiants n'ont pas tous la même question ...et surtout pas les mêmes réponses. Ici les paramètres sont 3 et 9 plutôt que 5 et 25.
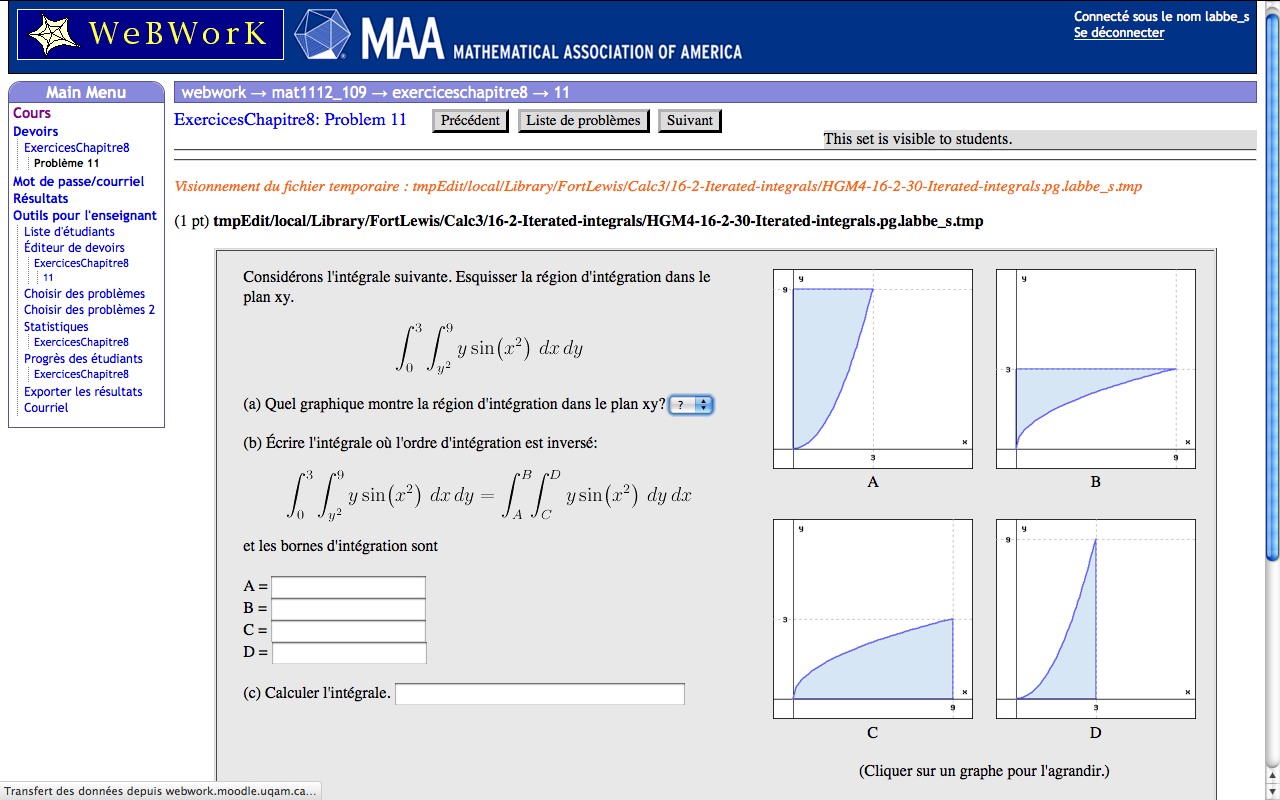
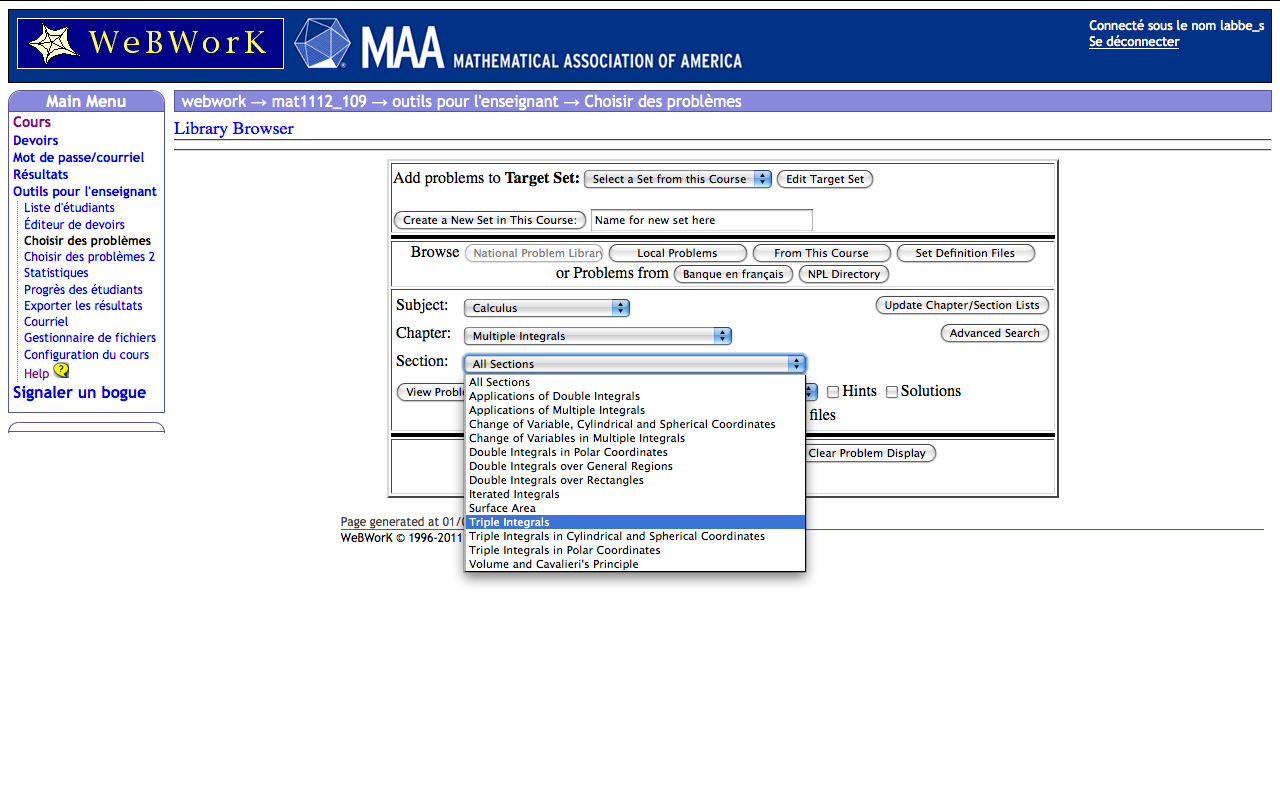
Choisir des problèmes par sujet:
La banque de plus de 20000 problèmes est divisée en sujets, chapitres et sections:
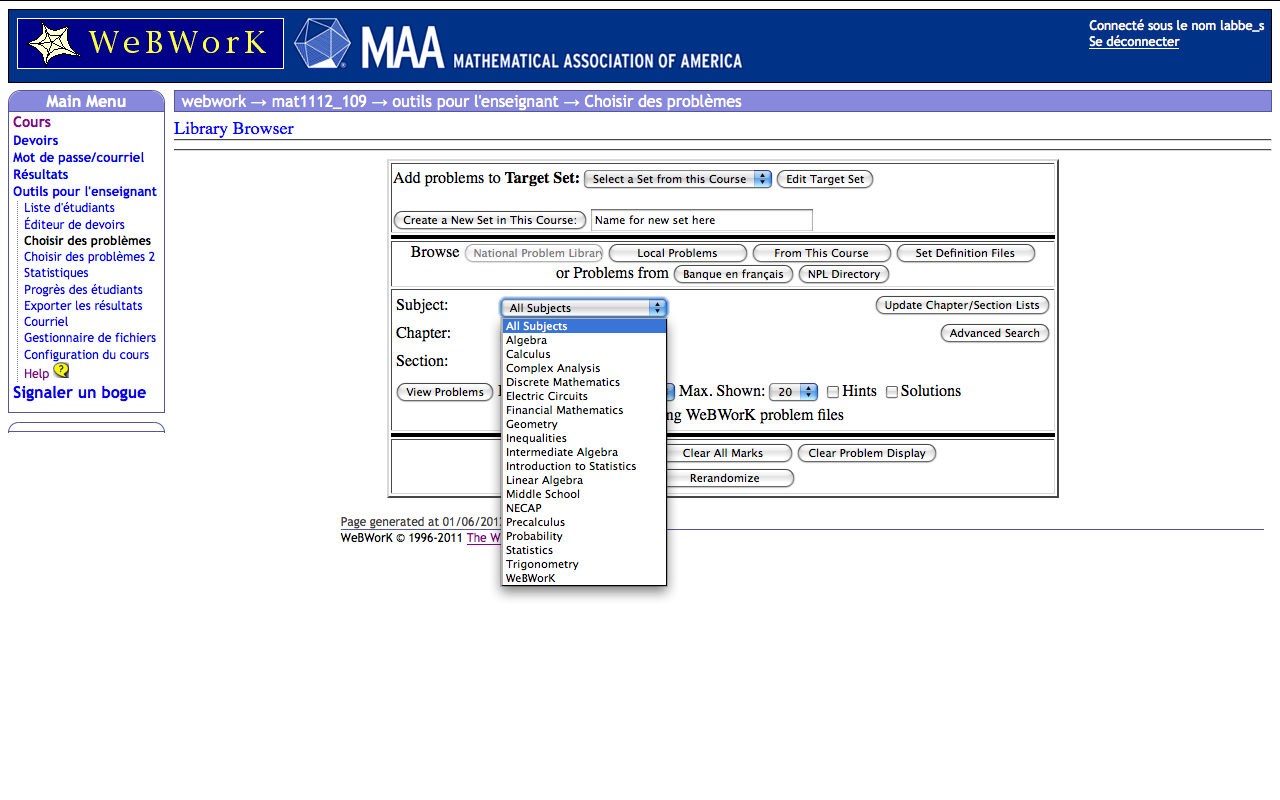
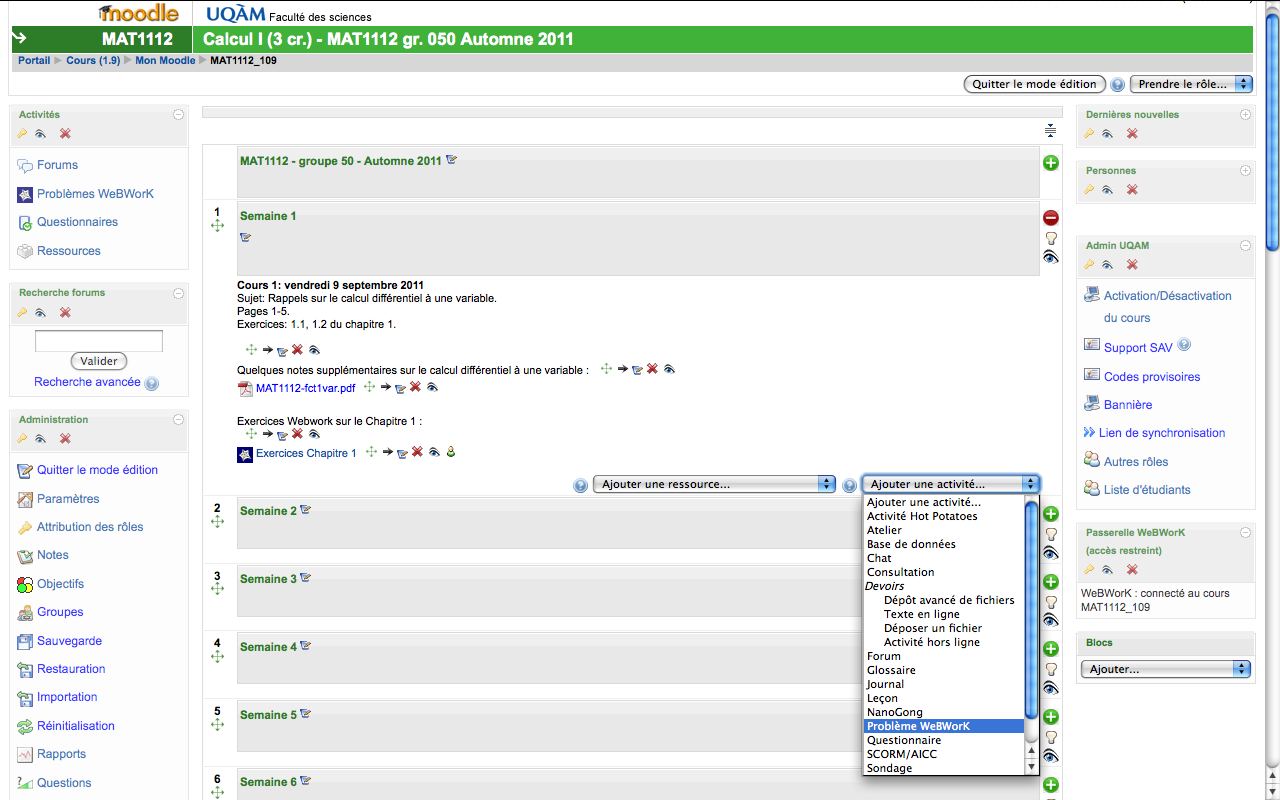
Publication d'exercices WeBWorK dans Moodle:
Le menu Ajouter une activité permet d'ajouter un lien vers les exercices WeBWorK.
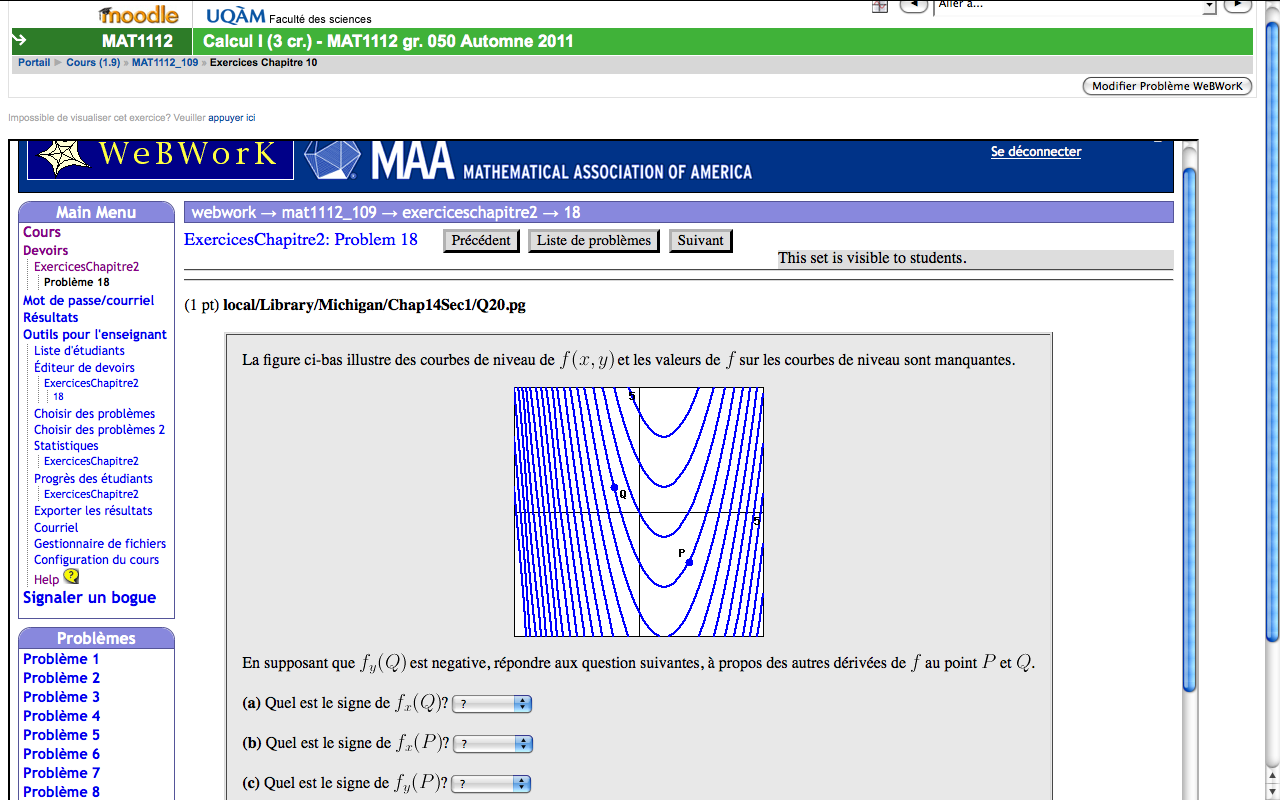
Exercices WeBWorK dans Moodle:
L'étudiantE accède aux exercices directement dans son compte Moodle.
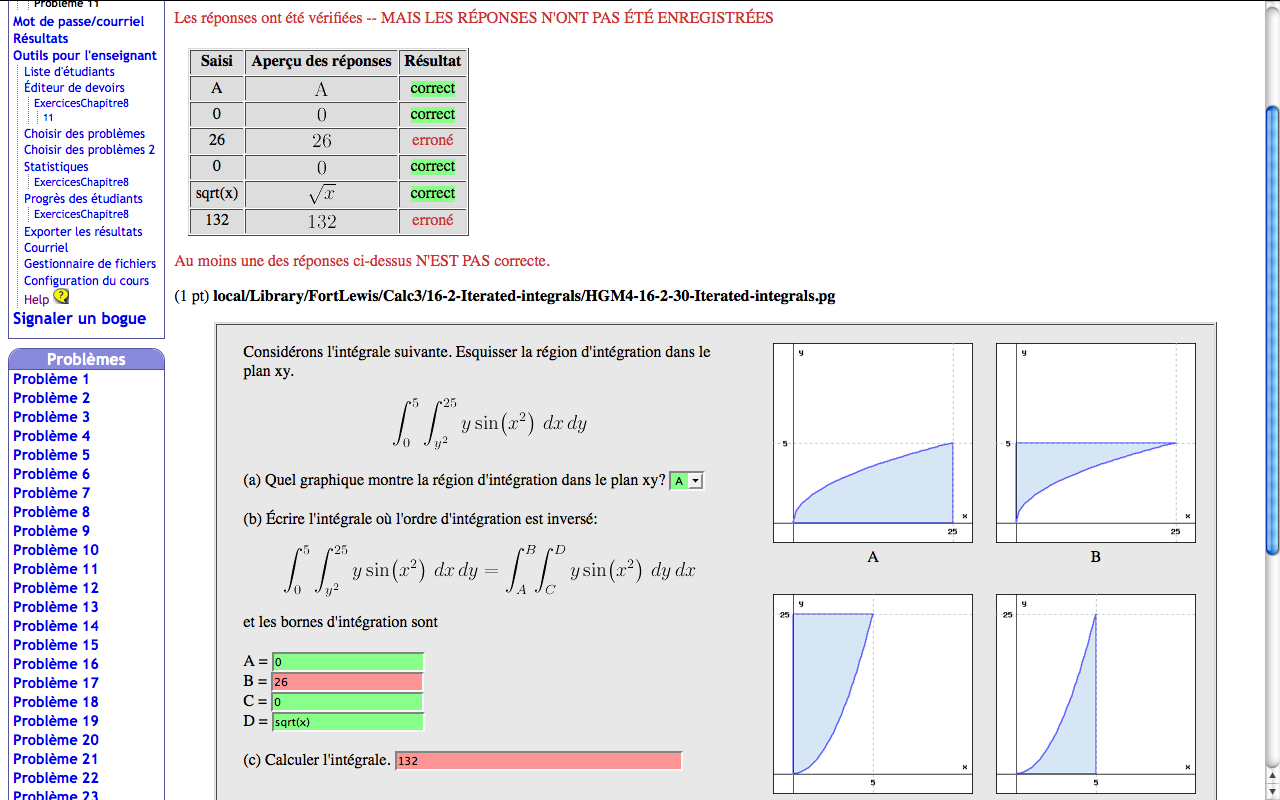
Vérifier les réponses:
L'étudiantE peut vérifier ses réponses mais n'obtient pas la réponse. En cas d'erreur, il ou elle doit réfléchir et corriger l'erreur.
Avantages
En tant qu'enseignant, j'y vois au moins deux avantages. Premièrement, cet outil peut être utilisé pour faire des évaluations plus fréquentes sans augmenter la tâche de correction qui se fait automatiquement. Par exemple, quelques questions par semaine peuvent être évaluées et compter pour 5% de la pondération. Deuxièmement, il est plus facile de traduire une question en français que d'en écrire une à partir de rien. À l'automne 2011, j'ai traduit 152 questions en français ce qui a offert une offre complémentaire d'exercices surtout pour la première moitié du cours où les exercices dans les notes de cours étaient considérés difficiles par les étudiantEs.
Questions aléatoires
Particularité intéressante, les paramètres dans les questions WeBWorK sont aléatoires de sorte que chaque étudiant reçoit une question différente. Si les étudiants se consultent, ils ne pourront pas copier la réponse et devront nécessairement discuter de la méthode ce qui est une bonne chose.
Alternatives commerciales
WeBWorK est un logiciel libre et gratuit de même que la banque de plus de 20000 problèmes qui l'accompagne. Or, il existe aussi des alternatives commerciales et payantes sur le marché. Par exemple, Maplesoft ont développé l'outil Maple T.A. pour créer des tests et des devoirs en ligne et évaluer automatiquement les réponses des élèves. Maple T.A. est présentement utilisé au Québec et a été présenté par Louise Pellerin et Diane Bergeron lors du 55e congrès de l'Association mathématique du Québec tenu les 14 et 15 octobre 2011 à l'École Polytechnique de Montréal. Elles l'utilisent respectivement au Cégep de Chicoutimi et à La Cité collégiale d'Ottawa pour diagnostiquer et exercer les étudiants dans l'apprentissage des mathématiques. Pour en savoir plus sur leur expérience, on peut lire cet article ou celui-ci sur le site de Profweb.
Combien coûte Maple T.A? En négociant avec Maplesoft, et aussi comme elles ont participé à la traduction de l'outil, elles ont obtenu un bon prix : entre 12$ et 18$ par licence (comprendre par étudiant) par année, le coût variant selon le nombre d’étudiants. Au début, ce coût était par session... Ainsi, pour le seul cours que j'ai donné à l'automne 2011, cela aurait coûté plus de 1000$ pour utiliser Maple T.A. plutôt que WeBWorK.
En discutant avec Mmes Pellerin et Bergeron, elles connaissaient l'existence de WeBWorK et gardent un oeil ouvert sur son développement et sur la traduction de son interface en français, car étant gratuit il sera toujours une option intéressante.
Service de l'audiovisuel de l'UQAM
Durant l'automne 2011, le projet WeBWorK a été repéré par le Service de l'audiovisuel de l'UQAM dont la mission est d’offrir une expertise et un soutien professionnel aux membres de la communauté universitaire dans la réalisation de leurs projets technopédagogiques ainsi que dans l’utilisation des technologies audiovisuelles et multimédias pour leurs activités d’apprentissage, d’enseignement, de recherche et de création. J'ai rencontré Marina Caplain en octobre sur le sujet. Si le projet se poursuit, ils pourront offrir un soutien aux utilisateurs.
Sondage des étudiantEs
À la fin du cours, en décembre 2011, j'ai fait un petit sondage par rapport à l'utilisation de WeBWorK. Une dizaine d'étudiantEs y ont répondu. En général, ceux qui ont utilisé WeBWorK ont trouvé que les exercices WeBWorK avaient eu un effet positif sur leur étude. Parmi les effets positifs on retrouve :
- "l'accès une plus grande variété de problèmes"
- "motivant de savoir directement si on avait la bonne réponse"
- "permettent de savoir si nous avons compris ou non la matière"
- "une façon plus divertissante de faire des problèmes mathématiques"
Parmi les effets négatifs on retrouve :
- "La démarche n'est pas considérée. Une démarche bien réalisée, avec une erreur de calcul, et la réponse peut différer complètement"
- "Beaucoup trop d'exercices à faire (exercices de l'imprimé de cours en plus des WeBWorK) et je ne savais donc pas lesquels étaient plus importants ou intéressants à faire et à comprendre."
La traduction
Voici quelques informations supplémentaires pour donner une meilleure idée de la tâche de traduction des questions. Chaque question est dans un fichier texte. Le fichier comporte une en-tête particulière décrivant le problème, puis un peu plus bas dans le fichier on retrouve le texte de la question:
BEGIN_TEXT
\{
ColumnTable(
"Consider the following integral. Sketch its region of integration in the xy-plane.".
$PAR.
$BCENTER.
"\( \displaystyle
\int_{0}^{$a} \int_{y^2}^{$a2} $f \, dx \, dy
\)".
$ECENTER.
$PAR.
"(a) Which graph shows the region of integration in the xy-plane? ".
$popup->menu().
$BR.
$BR.
"(b) Write the integral with the order of integration reversed:".
$PAR.
$BCENTER.
"\( \displaystyle
\int_{0}^{$a} \int_{y^2}^{$a2} $f \, dx \, dy
=
\int_{A}^{B} \!\! \int_{C}^{D} $f \, dy \, dx
\)".
$ECENTER.
$PAR.
"with limits of integration".
$BR.
$BR.
"A = ".ans_rule(20).$BR.
"B = ".ans_rule(20).$BR.
"C = ".ans_rule(20).$BR.
"D = ".ans_rule(20).$BR.
$BR.
"(c) Evaluate the integral. ".
ans_rule(40),
Dans ce cas-ci, j'ai édité une copie de ce fichier et j'ai remplacé le texte anglais par le texte français comme ci-bas:
BEGIN_TEXT
\{
ColumnTable(
"Considérons l'intégrale suivante. Esquisser la région d'intégration dans le plan xy.".
$PAR.
$BCENTER.
"\( \displaystyle
\int_{0}^{$a} \int_{y^2}^{$a2} $f \, dx \, dy
\)".
$ECENTER.
$PAR.
"(a) Quel graphique montre la région d'intégration dans le plan xy? ".
$popup->menu().
$BR.
$BR.
"(b) Écrire l'intégrale où l'ordre d'intégration est inversé:".
$PAR.
$BCENTER.
"\( \displaystyle
\int_{0}^{$a} \int_{y^2}^{$a2} $f \, dx \, dy
=
\int_{A}^{B} \!\! \int_{C}^{D} $f \, dy \, dx
\)".
$ECENTER.
$PAR.
"et les bornes d'intégration sont".
$BR.
$BR.
"A = ".ans_rule(20).$BR.
"B = ".ans_rule(20).$BR.
"C = ".ans_rule(20).$BR.
"D = ".ans_rule(20).$BR.
$BR.
"(c) Calculer l'intégrale. ".
ans_rule(40),
Durant la session, je parvenais à choisir et traduire une quinzaine de questions en un peu plus d'une heure de travail.
Conclusion
À mon avis, WeBWorK ne peut pas remplacer les devoirs écrits qui sont nécessaires pour évaluer la démarche, mais peut être un bon outil pour faire des évaluations plus fréquentes de la matière.
Modification du script tikz2pdf de Hans Meine
12 décembre 2011 | Catégories: latex | View CommentsIl y a deux raisons pour externaliser des images tikz d'un fichier .tex. La première est que les images tikz prennent parfois beaucoup de temps à compiler. La deuxième est que certains éditeurs n'acceptent pas les images tikz. Il faut donc trouver une manière de les transformer en format .pdf.
Ce processus d'externalisation est rendu possible grâce à la librairie external écrite par Christian Feuersänger, auteur de pgfplots. Cette librairie est pratique et atteint l'objectif, mais la création des images pdf dépend toujours du fichier principal.
En faisant une recherche du mot clé tikz2pdf dans Google, je suis tombé sur la page web de Hans Meine qui répond exactement à cette question.
Pour certaines raisons, le script de Hans Meine crée un fichier nommé tikz2pdf_temp.pdf. De plus, par défaut, le script cherche pour des modfications du fichier et exécute une recompilation automatiquement. Comme je n'aimais pas ces comportements, je les ai changés. La version modifiée du script tikz2pdf est disponible ici.
Retour sur la Conférence Ultimate Canada
23 novembre 2011 | Catégories: ultimate | View CommentsLes 18, 19 et 20 novembre dernier avait lieu la Conférence annuelle d'Ultimate Canada à Québec. C'était la première fois que j'y participais. J'ai fait une présentation sur l'ultimate 4 contre 4 au Québec que vous pouvez visionner ici :
4 on 4 Ultimate Tournaments in Quebec
Pendant la conférence, j'ai discuté avec de nouvelles personnes et appris de nouvelles choses. Dans ce message, je vais essayer de résumer ce que j'ai appris.
Ces dernières années, j'avais réalisé que le site web de The British Columbia Disc Sport Society n'avait pas tellement évolué, que les mises à jour étaient peu fréquentes et que des liens étaient souvent obsolètes. Je trouvais cela curieux, car la Colombie-Britanique est une région leader dans l'organisation de compétitions d'ultimate internationales et dans le développement de joueurs d'ultimate et d'équipes de haut niveau. J'ai donc posé la question à Jon Hayduk présent à la conférence. Jon joue avec Furious George et s'implique beaucoup dans le développeemnt junior là-bas. Sa réponse m'a surpris.
En Colombie-Britanique, la fédération provinciale chapeaute non seulement l'ultimate, mais aussi tous les sports de disque volant dont le disque golf. Cela est plutôt naturel, car plusieurs fédérations à l'international englobent aussi tous les sports de disque volant comme la World Flying Disc Federation, la France Flying Disc Federation et la Ontario Disc Sports Association. Au Québec, on ne connaît pas trop ce mode de fonctionnement. Les associations régionales québécoises sont des associations d'ultimate, de même pour la Fédération québécoise d'ultimate pour Ultimate Canada et pour USA Ultimate.
Or, il semble qu'on ait fait un bon choix au Québec, car depuis plusieurs mois, la fédération de Colombie-Britanique éprouve des problèmes de politique interne. En gros, la proportion du nombre du joueurs d'ultimate (plus de 80 %) n'est pas respecté au niveau budgétaire ni au niveau démocratique à l'interne. Ces divisions durent depuis plus de deux ans. Certains veulent se séparer, certains désirent le statu quo. Le problème n'est toujours pas réglé et les discussions se poursuivent. Or, pendant ce temps, leur énergie n'est pas investie sur les bonnes choses. Ils veulent changer le site web, mais ne veulent pas non plus avoir à tout refaire si jamais la fédération implose... Bref, plusieurs dossiers stagnent.
Une situation similaire a lieu en Ontario. J'ai discuté avec Jon Unger Brandt, président de l'ODSA. Environ 90% des membres de la fédération sont des joueurs d'ultimate, mais ils sont représentés à seulement 50% sur le conseil d'administration. À long terme, cela cause des tensions. Sans parler du fait que ni Ottawa ni Toronto ne sont membres de la fédération ontarienne. Il manque donc les deux plus grosses associations de l'Ontario.
Ainsi, on peut dire que l'ultimate au Québec est en plutôt bonne santé. Les associations sont en bonnes relations entre elles et aussi avec la Fédération. Cette bonne entente est propice au développement, car toute l'énergie va à la bonne place. Je vous le confirme, les Canadiens l'ont remarqué.
Dimanche, nous avons réalisé une entrevue avec Jon Hayduk à propos du passage au niveau canadien de la catégorie junior du jeu mixte vers le jeu masculin et le jeu féminin. Vous pouvez visionner l'entrevue ici :
http://vimeo.com/32569475
Après avoir essayé le format 4 contre 4, Jon Hayduk disait qu'il y a trop de pause. Il préfère le jeu à la volée, donc sans validation par la défensive après un point. En effet, on pourrait essayer et voir la différence. Mais, bon, s'il n'y avait pas d'arrêts de jeu au tennis, je ne sais pas si Nadal pourrait jouer en se donnant autant du début à la fin...
La présentation du conférencier invité Charles Cardinal était excellente. Il a parlé du développement à long terme de l'athlète. Personnellement, j'ai appris beaucoup. C'est impossible à résumer ce que j'ai appris ici, ce serait trop long. Il nous a mentionné le site web suivant où on peut trouver des documents très bien faits sur le sujet :
Au Canada, le sport c'est pour la vie
Il nous a aussi mentionné qu'il faut miser sur l'aspect esprit du jeu et communautaire pour se différencier des autres sports et faire notre entrée dans le sport scolaire.
Utiliser les raccourcis vi dans la ligne de commande Sage
21 novembre 2011 | Catégories: terminal, sage, vim | View CommentsPar défaut, le terminal utilise les raccourcis emacs. Par exemple, CTRL-A pour aller au début de la ligne et CTRL-E pour aller à la fin de la ligne. Pour utiliser plutôt les raccourcis vi, il suffit de taper la commande suivante dans le terminal:
set -o vi
Par contre, ceci ne change pas le mode utilisé par la ligne de commande du logiciel Sage. Pour y parvenir, il faut plutôt ajouter les lignes suivantes dans le fichier ~/.inputrc:
set editing-mode vi set keymap vi-insert
Autre que l'option vi-insert, on peut également écrire vi ou vi-command pour la ligne set keyamp, mais je n'ai pas encore vu réellement une différence, car il semble toujours que le mode insertion est utilisé par défaut. On peut trouver plus d'informations sur le sujet ici:
http://vim.wikia.com/wiki/Use_vi_shortcuts_in_terminal
Recherche dans l'historique selon le préfixe
Tant qu'à y être, on peut en profiter pour activer une fonctionalité pour le terminal plutôt pratique qui est activée par défaut en Sage. Dans la ligne de commande Sage, en utilisant les flèches HAUT et BAS, on peut faire une recherche dans l'historique parmi les commandes ayant un préfixe commun avec le préfixe à gauche de la position du curseur. Pour activer cette fonctionalité dans le terminal, il suffit d'ajouter les deux lignes suivantes au même fichier ~/.inputrc:
"\e[A": history-search-backward # up-arrow "\e[B": history-search-forward # down-arrow
Merci à Franco Saliola de m'avoir partagé ces solutions.
Résoudre le puzzle Quantumino avec le logiciel Sage
14 novembre 2011 | Catégories: sage | View CommentsLe 29 octobre dernier, la version 4.7.2 de Sage est sortie. C'est dans cette version de Sage (merci beaucoup à Rob Beezer qui a arbitré cette contribution) qu'a été ajouté le code que j'ai écrit en juin dernier pour résoudre le puzzle appelé Quantumino. Ce puzzle avait été laissé à la salle à manger du Laboratoire de Combinatoire Informatique Mathematique de Montréal par Franco Saliola durant l'hiver 2011...

- Puzzle Quantumino par Family Games America
- Quantumino sur Youtube
La solution utilise le code des liens dansants qui se trouvait déjà dans Sage pour résoudre le problème du Sudoku. Les liens dansants ont été introduits par Donald Knuth en 2000 pour résoudre le pavage d'une région 2D par des pentaminos. Ici nous utilisons la même méthode en dimension quelconque et nous l'appliquons pour résoudre le puzzle Quantumino. Voici les deux pages concernées de la documentation de Sage:
Voici les 17 blocs de bois du puzzle Quantumino:
sage: from sage.games.quantumino import show_pentaminos sage: show_pentaminos()

Pour résoudre le puzzle où le pentamino numéroté 7 est mis de côté:
sage: from sage.games.quantumino import QuantuminoSolver sage: s = QuantuminoSolver(7).solve().next() sage: s.show3d().show(frame=False)

Pour obtenir d'autres solutions, utilisez l'itérateur retourné par la fonction solve. Notez que trouver la première solution est plus long car on a besoin de créer les données complètes pour décrire le problème:
sage: it = QuantuminoSolver(7).solve() sage: 1st_solution = it.next() sage: 2nd_solution = it.next() sage: 3rd_solution = it.next() sage: 3rd_solution.show3d().show(frame=False)
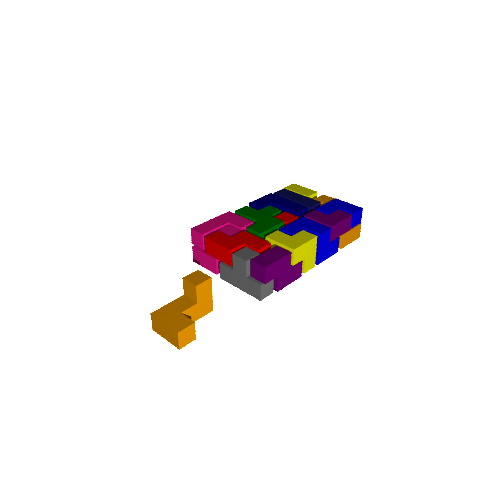
Pour obtenir la solution à l'intérieur d'autres boîtes:
sage: s = QuantuminoSolver(7, box=(4,4,5)).solve().next() sage: s.show3d()

S'il n'y a pas de solution, l'itération se termine immédiatement:
sage: QuantuminoSolver(7, box=(3,3,3)).solve().next() Traceback (most recent call last): ... StopIteration
Si vous êtes patients, vous pouvez essayer de calculer le nombre de solutions. Attention, il y en a beaucoup!:
sage: from sage.games.quantumino import QuantuminoSolver sage: q = QuantuminoSolver(7) sage: q.number_of_solutions() # prendra plusieurs jours de calculs
Le code permet aussi l'introspection. À partir d'un objet de la classe sage.combinat.tiling.TilingSolver, il est possible de récupérer les lignes de la matrice décrivant le problème de couverture exacte en question. Il est également possible d'obtenir une instance du solveur DLX et de tester certaines choses:
sage: q = QuantuminoSolver(0) sage: T = q.tiling_solver() sage: T Tiling solver of 16 pieces into the box (5, 8, 2) Rotation allowed: True Reflection allowed: False Reusing pieces allowed: False sage: rows = T.rows() sage: len(rows) 5484 sage: x = T.dlx_solver() sage: x <sage.combinat.matrices.dancing_links.dancing_linksWrapper object at ...>
« Previous Page -- Next Page »
