Il existe une méthode peu connue pour connaître les composantes de Sage utilisées par un calcul. Supposons qu'on a le calcul suivant:

sage: g = Permutation('(2,3)')
sage: h = Permutation('(2,3,4,5)')
sage: S = PermutationGroup([g, h])
sage: c = S.conjugacy_classes_subgroups()

Pour connaître les systèmes utilisés par le calcul précédent, on écrit:

sage: import sage.misc.citation
sage: sage.misc.citation.get_systems('S.conjugacy_classes_subgroups()')
['GAP']

Cela permet de savoir par exemple quels systèmes on doit citer dans un article de recherche qui les utilise. Voici un autre exemple qui montre que quatre systèmes sont utilisés pour calculer l'intégrale \(\int \cos(x^2) dx\):

sage: from sage.misc.citation import get_systems
sage: get_systems("integrate(cos(x^2), x)")
['MPFI', 'ginac', 'GMP', 'Maxima']

L'existence de la fonction get_systems a été rappelée en juillet 2011 par Mike Hansen dans cette conversation sur sage-devel : Citing used Sage components automatically.

In Sage, we can create 3d graphic objects like the following:

sage: a = line3d([(0,1,0), (0,0,0), (1,0,0), (2,0,0)], radius=0.1)
sage: b = line3d([(1,0,0), (1,0.5,0)], radius=0.1)
sage: g = a + b

sage: x,y = map(vector, g.bounding_box())
sage: g.frame_aspect_ratio(tuple(y-x))      # this sets the aspect ratio to 1

sage: g

Rotate the graphic object until you get a view you like.

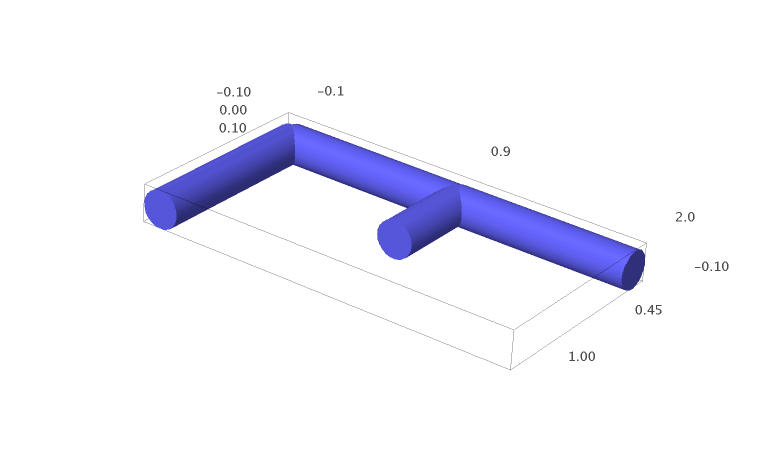
One can save an image as a jpg, but the quality is not always good and one could prefer to draw the image using another tool like tikz code. But how to draw the 3d graphic object with the same projection?

To get information about the actual view and hopefully about the camera position, right clic on the image and go to the current state ("État courant" in French).

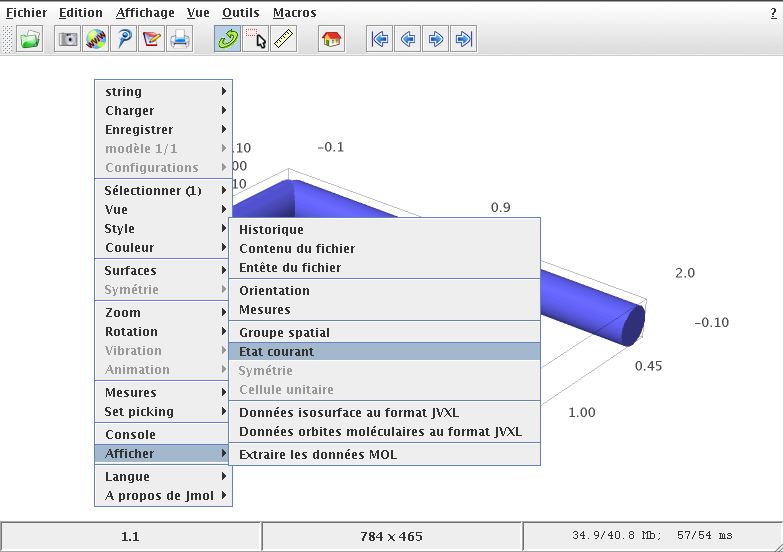
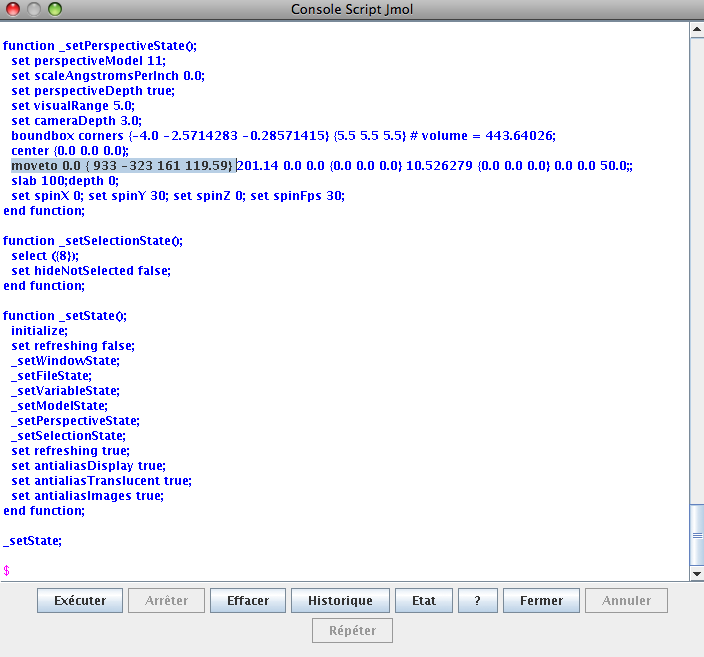
In the window that pops up, the information you need is the line starting with:

moveto 0.0 {933 -323 161 119.59}

According to the Jmol documentation of the moveto method (and also after doing some moveto tests in the script window), I understand that this tells that a rotation of angle \(119.59\) degrees is done on the axis \((933, -323, 161)\). The rotation is done counterclockwise (right-hand rule). From this information, we may then compute the rotation matrix using rotate_arbitrary method written by Robert Bradshaw and available in Sage. Note that the rotation of the method rotate_arbitrary is done counterclockwise (left-hand rule).

sage: from sage.plot.plot3d.transform import rotate_arbitrary
sage: v = (933, -323, 161)
sage: angle = 119.59                    # righ-hand rule
sage: angle = - angle                   # left-hand rule
sage: angle_rad = angle * pi / 180
sage: M = rotate_arbitrary(v, angle_rad)
sage: M
[  0.805577517225  -0.589785522899 -0.0565499842683]
[  -0.30988380511  -0.338059560724  -0.888643776062]
[  0.504991971294   0.733395371121  -0.455098163637]

Since the default position of the camera is on the positive Z axis, one can find the actual position of the camera by doing the inverse of the rotation on the vector \((0,0,1)\):

sage: camera = ~M * vector((0,0,1))
sage: camera
(0.504991971294, 0.733395371121, -0.455098163637)

To draw the same plot with the same angle of view in tikz, one needs the proper projection matrix:

sage: projection = M[:2]
sage: projection
[  0.805577517225  -0.589785522899 -0.0565499842683]
[  -0.30988380511  -0.338059560724  -0.888643776062]

One may test that this projection is really parallel to the segment that joins the origin to the camera:

sage: projection * camera
(5.55111512313e-17, 0.0)

The part of tikz code that gives the projection information is:

sage: s = '['
sage: s += 'x={(%scm, %scm)},\n' % tuple(projection * vector((1,0,0)))
sage: s += 'y={(%scm, %scm)},\n' % tuple(projection * vector((0,1,0)))
sage: s += 'z={(%scm, %scm)}'    % tuple(projection * vector((0,0,1)))
sage: s += ']'
sage: print s
[x={(0.805577517225cm, -0.30988380511cm)},
y={(-0.589785522899cm, -0.338059560724cm)},
z={(-0.0565499842683cm, -0.888643776062cm)}]

The complete tikz code is:

\begin{tikzpicture}
[x={(0.805577517225cm, -0.30988380511cm)},
y={(-0.589785522899cm, -0.338059560724cm)},
z={(-0.0565499842683cm, -0.888643776062cm)}, scale=3]
\draw[blue,line width=.4cm] (0,1,0) -- (0,0,0) -- (1,0,0) -- (2,0,0);
\draw[blue,line width=.4cm] (1,0,0) -- (1,0.5,0);
\end{tikzpicture}

The generated tikz image (pdf converted to a png: sorry for the bad quality) is:

One can verified that it has the same view as the original Jmol view.

Thanks to my brother Jean-Philippe who tested this method.

MathJax est un logiciel libre qui permet d'afficher des formules mathématiques dans une page web et qui fonctionne quelque soit le navigateur utilisé.

MathJax se veut le successeur de JsMath tous deux développés principalement par David P. Cervone. Pour Cervone, il était important que le projet survive en son absence (on se sait jamais ce que la vie nous réserve) et ne dépende pas que de lui. Ainsi, il s'est assuré d'avoir les appuis nécessaires : le projet est notamment parrainé par l'American Mathematical Society et est soutenu par l'American Physical Society, Elsevier et le projet Euclide. Les sites web MathSciNet et MathOverflow utilisent maintenant MathJax.

Pour utiliser MathJax dans cette page, j'ai copié les lignes suivantes dans le code de la page:

<script type="text/x-mathjax-config">
  MathJax.Hub.Config({
    extensions: ["tex2jax.js"],
    jax: ["input/TeX", "output/HTML-CSS"],
    tex2jax: {
      inlineMath: [ ["\\(","\\)"] ],
      displayMath: [ ["\\[","\\]"] ],
      processEscapes: true
    },
    "HTML-CSS": { availableFonts: ["TeX"] }
  });
</script>
<script type="text/javascript"
src="http://cdn.mathjax.org/mathjax/latest/MathJax.js"></script>

Ainsi, des formules telles que:

Of a set \(\mathcal{S}\) is a bijection \(\psi : \mathcal{S} \rightarrow \mathcal{S}\).

se transforment en:

Of a set \(\mathcal{S}\) is a bijection \(\psi : \mathcal{S} \rightarrow \mathcal{S}\).

Autres exemples:

\(\pi = \frac{C}{d}\) devient \(\pi=\frac{C}{d}\)

\(\int\cos(x) dx = \sin(x) + K\) devient \(\int\cos(x) dx = \sin(x) + K\)

On peut changer les options d'affichage des formules en faisant un clic-droit sur les formules. Par exemple, je trouve que le résultat est plus beau lorsque HTML-CSS est utilisé plutôt que MATHML. On peut changer ce paramètre dans allant dans Settings -> Math Renderer. Par contre, HTML-CSS est un peu plus long à charger.

Le système de pointage du Circuit québécois d'ultimate 4 contre 4 pour la saison 2010-2011 était le suivant:

• Série A: Movember, Bye Bye, La Flotte, Coup de Foudre, Mars Attaque
• Série B: OctoberDisk, Fun-E-nuF, La Virée

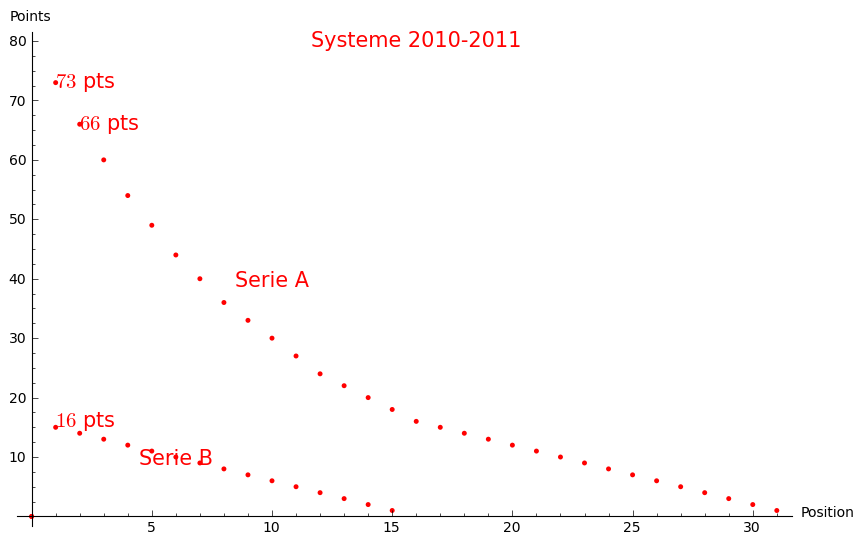
Une échelle allant de 1 à 73 points était utilisée pour les tournois de série A et donnait des points à 31 équipes. Une échelle de 1 à 16 points était utilisée pour les tournois de série B et donnait des points à 16 équipes. Ces échelles de pointages avaient été conçues à l'automne 2007 à une époque où le plus grand tournoi acceptait 36 équipes. Vu l'augmentation de popularité du circuit (le nombre d'équipes participant au circuit a doublé en trois ans), le système de pointage doit être actualisé. Notamment, sur les 88 équipes ayant participé au tournoi Mars Attaque en mars 2011, seules 31 équipes ont reçu des points et 57 équipes ont obtenu un pointage de zéro. De plus, à cause de l'ajout d'un tournoi de série A à Montréal, plusieurs équipes ont fait le choix de ne pas participer au tournoi La Flotte de Rimouski ce qui a créé un déséquilibre dans le système.

Ainsi, le système doit être actualisé pour deux raisons : (1) donner des points à toutes les équipes et (2) équilibrer le système en fonction de la force des tournois.

Plusieurs discussions ont eu lieu à ce sujet au cours des derniers mois. Certaines personnes ont suggéré de modifier complètement le système. Certains ont mentionné l'idée de ligue, etc. Dans ce message, je propose un système en continuité avec celui utilisé au cours des dernières années. À mon avis le système utilisé depuis le début va plutôt bien, on doit simplement l'actualiser.

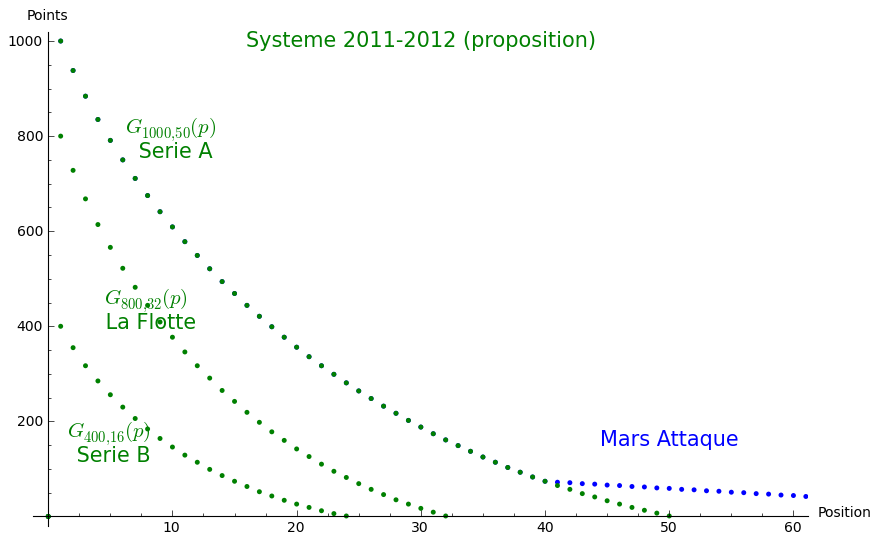
En s'inspirant du système de l'ATP où le gagnant d'un tournoi obtient un nombre rond de points (ATP 1000 points, 2000 points, 500 points). Je propose de faire de même pour le CQU4. Ainsi, l'équipe gagnante d'un tournoi de série A obtiendra 1000 points et 400 points pour un tournoi de série B. Cinquante équipes obtiendront des points dans un tournoi de série A (sauf pour le Mars Attaque où l'échelle sera allongée) et 24 équipes obtiendront des points pour un tournoi de série B. Le tournoi La Flotte aura sa propre classe : 800 points pour l'équipe gagnante et 32 équipes obtiendront des points. Ainsi, l'équipe gagnante du tournoi La Flotte obtiendra autant de points qu'une 5e place dans un tournoi de série A ce qui correspond à la réalité. Les quatre tournois de série A seraient : Movember, Bye Bye, Coup de Foudre, Mars Attaque et les tournois de série B seraient : OctoberDisk, Fun-E-nuF, La Virée, Ottawa (nouveau) et Landaudière (nouveau). Cela est résumé dans l'image ci-bas:

Points d'esprit sportif

Trois équipes obtiennent 50 points pour les tournois de Série A et le tournoi La Flotte et une équipe obtient 50 points pour les tournois de Série B.

Somme des 3 meilleurs résultats

Pour calculer le nombre de points total d'une équipe, on fait la somme des trois meilleurs résultats comme par les années précédentes.

Les valeurs exactes des points selon les positions finales à chaque tournoi sont dans le tableau suivant.

On veut placer les pièces suivantes dans un carré 8 par 8.

En utilisant sage-4.7 muni des patchs du ticket #11379 et avec les commandes suivantes, on peut trouver une solution et même les calculer toutes:

sage: from sage.combinat.tiling import Polyomino, TilingSolver
sage: L = []
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)], 'yellow'))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)], "black"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)], "gray"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,3)],"cyan"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1)],"red"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,2)],"blue"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,3)],"green"))
sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)],"magenta"))
sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)],"orange"))
sage: L.append(Polyomino([(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)],"pink"))
sage: T = TilingSolver(L, (8,8), reflection=True)
sage: T.number_of_solutions()
328

Ainsi (sans tenir compte de la non adjacence des carrés blancs et noirs), il y a 328 solutions. Les voici en animation:

sage: a = T.animate()
sage: a
Animation with 328 frames
sage: a.show(delay=50, iterations=1)

Chaque solution est répétée 8 fois (les 4 rotations et les 4 rotations de l'image miroir), ainsi il n'y a que 41 solutions vraiment distinctes:

sage:: factor(328)
8 * 41

J'ai aussi codé:

sage: a = T.animate('incremental', stop=300)

où une seule pièce est enlevée ou ajoutée à la fois ce qui permet vraiment de visualiser les liens dansants de Knuth (rafraîchir le navigateur pour faire recommencer l'animation):