Animation des solutions d'un puzzle de Florent Hivert
22 juillet 2011 | Catégories: animation, sage | View CommentsOn veut placer les pièces suivantes dans un carré 8 par 8.
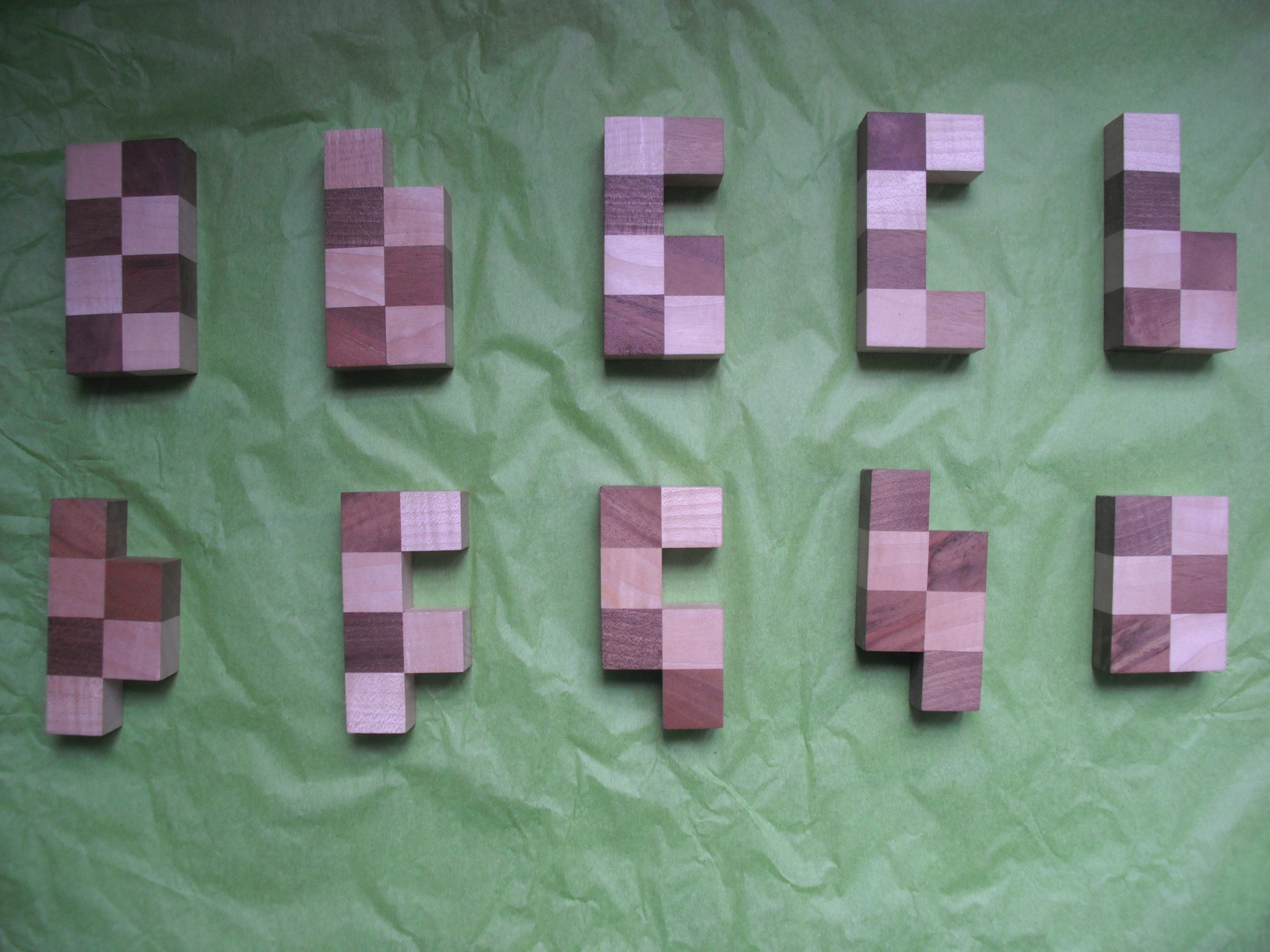
En utilisant sage-4.7 muni des patchs du ticket #11379 et avec les commandes suivantes, on peut trouver une solution et même les calculer toutes:
sage: from sage.combinat.tiling import Polyomino, TilingSolver sage: L = [] sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3)], 'yellow')) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)], "black")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)], "gray")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,3)],"cyan")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,0),(1,1)],"red")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,2)],"blue")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(0,3),(1,1),(1,3)],"green")) sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,3)],"magenta")) sage: L.append(Polyomino([(0,1),(0,2),(0,3),(1,0),(1,1),(1,2)],"orange")) sage: L.append(Polyomino([(0,0),(0,1),(0,2),(1,0),(1,1),(1,2)],"pink")) sage: T = TilingSolver(L, (8,8), reflection=True) sage: T.number_of_solutions() 328
Ainsi (sans tenir compte de la non adjacence des carrés blancs et noirs), il y a 328 solutions. Les voici en animation:
sage: a = T.animate() sage: a Animation with 328 frames sage: a.show(delay=50, iterations=1)

Chaque solution est répétée 8 fois (les 4 rotations et les 4 rotations de l'image miroir), ainsi il n'y a que 41 solutions vraiment distinctes:
sage:: factor(328) 8 * 41
J'ai aussi codé:
sage: a = T.animate('incremental', stop=300)
où une seule pièce est enlevée ou ajoutée à la fois ce qui permet vraiment de visualiser les liens dansants de Knuth (rafraîchir le navigateur pour faire recommencer l'animation):

ReST to Sage Worksheet
17 juin 2011 | Mise à jour: 08 septembre 2011 | Catégories: rst, sage | View CommentsDuring Sage Days 31, I worked on the ticket #11459 to implement rst to sws conversion. This post intends to give some documentation about this new feature. Here is an example of a ReStructuredText file calculus.rst:
********
Calculus
********
Let's do some calculus using Sage.
Differentiation
===============
The derivative of $\\sin(x)$ is::
sage: diff(sin(x), x)
cos(x)
The derivative of $\\log(x) + x^2$ is::
sage: diff(log(x) + x^2, x)
2*x + 1/x
Integration
===========
Sage can integrate $\\int x^3 dx$::
sage: f = x^3
sage: f.integral(x)
1/4*x^4
Let's compute $\\int x \\sin(x^2) dx$::
sage: f = x*sin(x^2)
sage: integral(f,x)
-1/2*cos(x^2)
Both the files calculus.rst and calculus.html, which was generated from the file calculus.rst using Docutils and the command rst2html.py calculus.rst calculus.html, can be uploaded into the Sage Notebook (copy their URL):
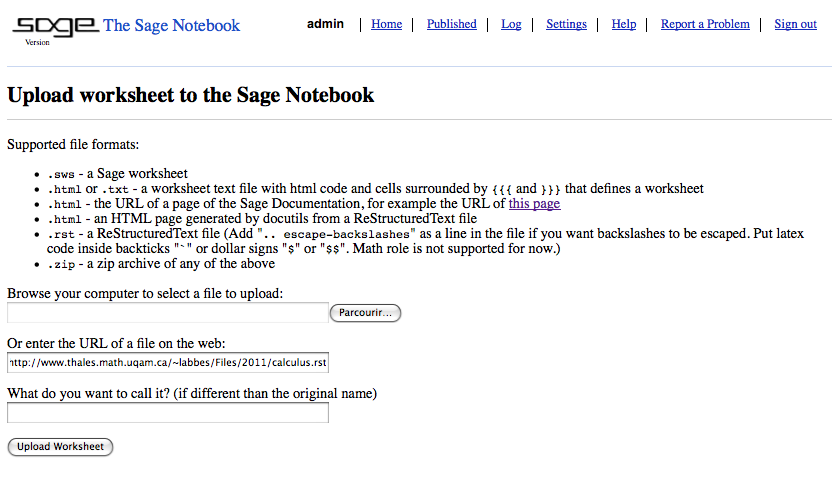
This will create a new worksheet:
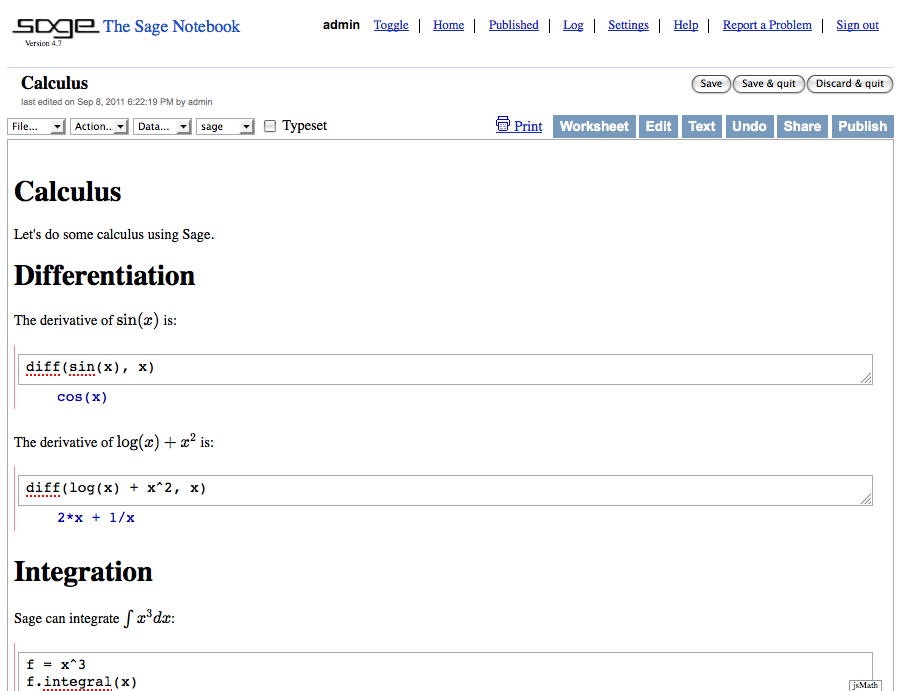
I also implemented two command line scripts to generate the worksheet text file:
sage -rst2txt file.rst file.txt
and to generate the Sage worksheet (.sws) directly:
sage -rst2sws file.rst file.sws
I also added the possibility to automatically escape every backslashes if they are not already so that they don't get lost in the translation process. For more info, consult the documentation:
sage -rst2txt -h sage -rst2sws -h
ReST syntax highlighting for Sage docstrings in VIM
15 juin 2011 | Catégories: sage | View Comments| Author: | Franco Saliola |
|---|---|
| Contact: | saliola at gmail dot com |
| Date: | 3 December 2010 |
Sage uses ReST syntax in its (Python) docstrings, but the default Python syntax highlighting in vim treats all docstrings as Python strings. Here is a method (by Franco Saliola) to enable ReST highlighting in the docstrings and highlighting of doctests.
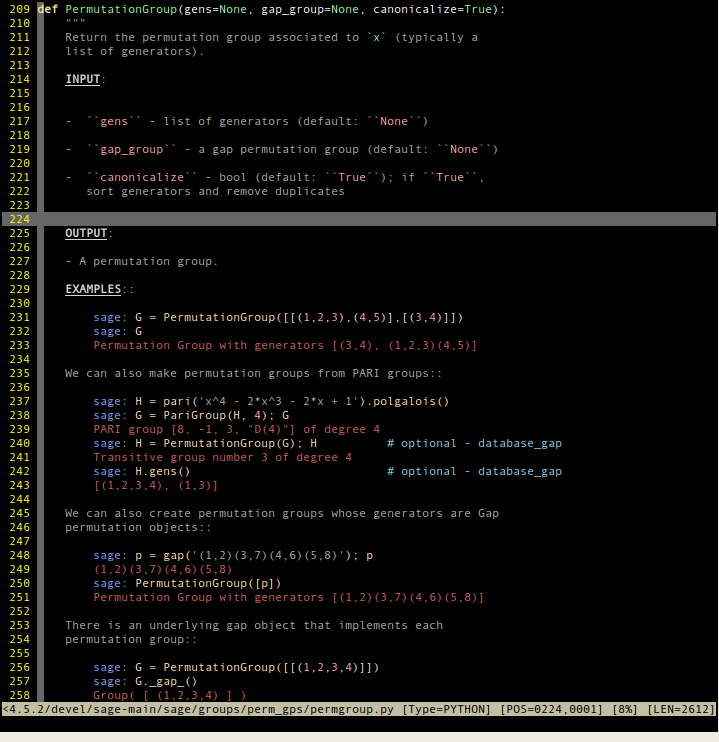
Prerequisites
The usual syntax files python.vim and rst.vim must be in the ~/.vim/syntax folder. You can find those on the web. Here is the rst.vim file made by Nikolai Weibull (latest revision: 2010-01-23).
Configuration
Create the directory:
mkdir -p ~/.vim/after/syntax
Any file in this directory will be loaded after the default syntax files, allowing us modify the default highlighting and add our own customizations.
Copy the file python.vim (which can be found in the same directory as this file) into the directory ~/.vim/after/syntax.
The first few lines of the file python.vim define the default colours for the docstring text, the sage keywords and the sage prompt. You might want to modify these to suit your colour scheme.
References
- http://www.mail-archive.com/vim_use@googlegroups.com/msg06545.html
- help :syn-include
Evolution of the overall doctest coverage of Sage
06 mars 2011 | Catégories: sage | View CommentsI just did a graph of the Evolution of the Overall Doctest Coverage of Sage since 3 years. The png is below.
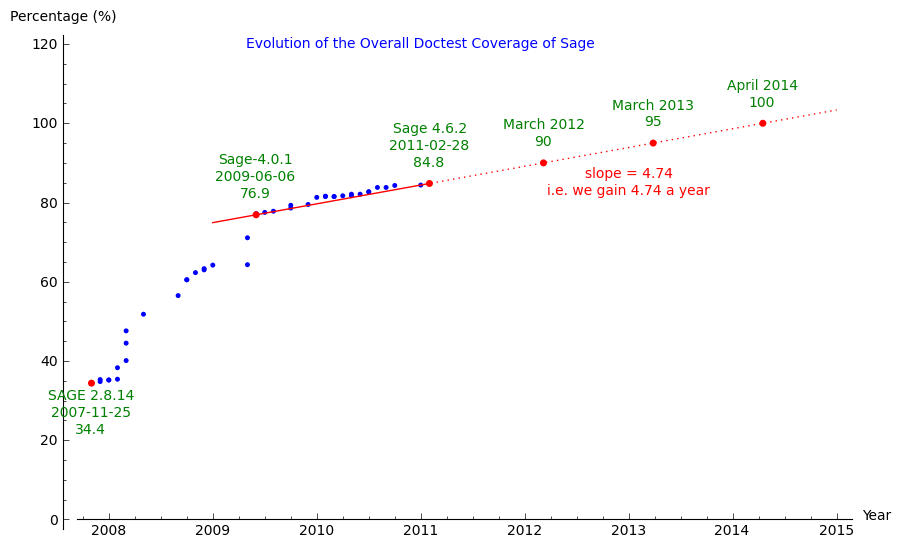
The coverage evolved quiet regularly during the last 20 releases (=20 months) with an average of a bit less than 5 percent a year. For sage-4.6.2, it is actually 84.8%. If we keep this rhythm, we should reach 90% coverage by March 2012 and 100% by April 2014.
The code I used is here : coverage_evolution.py.
Occurences of a certain factor in the Kolakoski word
16 février 2011 | Catégories: Kolakoski, sage | View CommentsThe factor 212212112112212112122112112212212112112212112122112112 occurs in the Kolakoski word at the positions 3190, 6366, 7614, 12950, 13765, 14277, 20385, 21344, 39674 and so on. The successive gaps of these first eight occurences are 3176, 1248, 5336, 815, 512, 6108, 959, 18330. Are the gap between all of these occurences bounded or not? The following table lists only the gap that are going increasingly for the Kolakoski word up to 100 billion (=10^9).
| i | ith occurence | (i+1)th occurence | gap |
| 0 | 3190 | 6366 | 3176 |
| 2 | 7614 | 12950 | 5336 |
| 5 | 14277 | 20385 | 6108 |
| 7 | 21344 | 39674 | 18330 |
| 8 | 39674 | 58946 | 19272 |
| 17 | 85963 | 107018 | 21055 |
| 225 | 945732 | 966924 | 21192 |
| 685 | 2832810 | 2858670 | 25860 |
| 822 | 3549762 | 3583161 | 33399 |
| 965 | 4188934 | 4223349 | 34415 |
| 1526 | 6773992 | 6809208 | 35216 |
| 7117 | 31279355 | 31320896 | 41541 |
| 18054 | 79167173 | 79213333 | 46160 |
| 20838 | 90761663 | 90809563 | 47900 |
| 176198 | 768146935 | 768195609 | 48674 |
| 292643 | 1278852293 | 1278906094 | 53801 |
| 554207 | 2424441033 | 2424495471 | 54438 |
| 590128 | 2581311276 | 2581367730 | 56454 |
| 948506 | 4150204101 | 4150264753 | 60652 |
| 1156072 | 5055131250 | 5055199553 | 68303 |
| 1514374 | 6620302433 | 6620372047 | 69614 |
| 11154155 | 48788048239 | 48788121823 | 73584 |
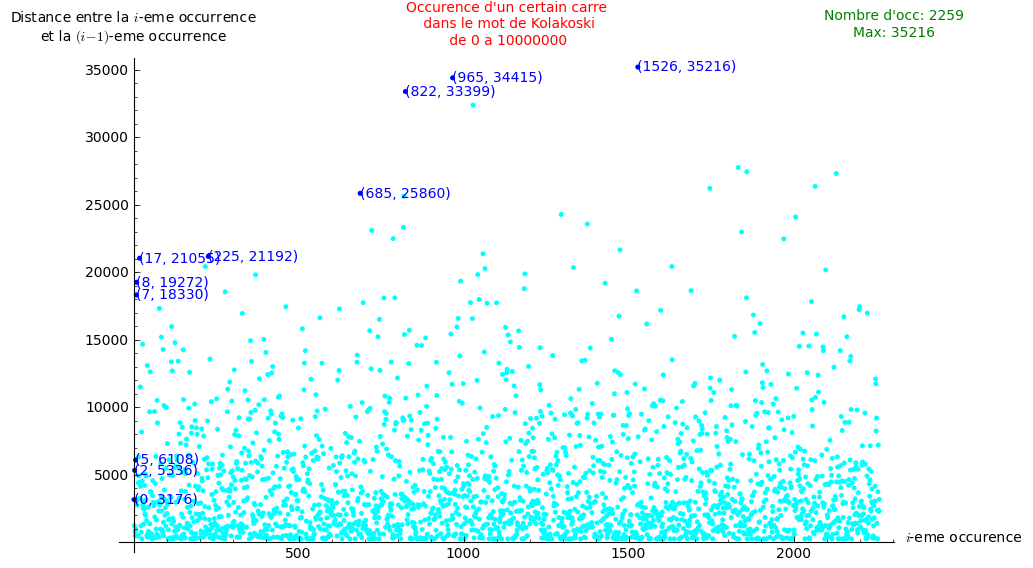
The following image draws all the gaps in function of i for the first 10 million digit.
« Previous Page -- Next Page »
