I am currently at Sage Days 28. Right now, there is a discussion about Analytic combinatorics in Sage and the new code written by Alex Raichev at tikcet #10519 was mentionned in the discussion. His code is a bunch of def python functions in a sage file. In Sage, code is written in object oriented way.

I am not an expert of the domain of analytic combinatorics, but I am coding oriented object Python since some time now. So I wrote a comment on the ticket gathering my thoughts to, I hope, help Alex to rewrite his set of functions into an oriented object structure. I copied the content of my comment below as it will be easier to share it.

r"""
[...]

This code relates to analytic combinatorics.
More specifically, it is a collection of functions designed
to compute asymptotics of Maclaurin coefficients of certain classes of
multivariate generating functions.

The main function asymptotics() returns the first `N` terms of
the asymptotic expansion of the Maclaurin coefficients `F_{n\alpha}`
of the multivariate meromorphic function `F=G/H` as `n\to\infty`.
It assumes that `F` is holomorphic in a neighborhood of the origin,
that `H` is a polynomial, and that asymptotics in the direction of
`\alpha` (a tuple of positive integers) are controlled by smooth
or multiple points.

[...]
"""

class HolomorphicMultivariateMeromorphicFunction(object):

    # Constructor of the object
    def __init__(self, F, G):
        #stores important information on the object as attributes of self
        self._F = F
        self._G = G

    def maclaurin_coefficients(self, n, alpha):
        r"""
        Return the maclaurin coefficients of self.

        INPUT:

        - ``alpha`` - tuple of positive integers

        OUTPUT:

        a python list of the first terms

        OR

        maybe an object of a class you implement if there exists pertinent
        questions to ask to it.
        """
        #Do some computations based (I guess) on self._F and self._G
        intermediate_result1 = self.some_intermediate_computations_1()
        #Do more computations
        return something

    def asymptotics(self, N, alpha):
        r"""
        Returns the asymptotics of Maclaurin coefficients.
        """
        #Do some computations based (I guess) on self._F and self._G
        intermediate_result2 = self.some_intermediate_computations_2()
        intermediate_result3 = self.some_intermediate_computations_3()
        return something

    #put here all the others functions needed to compute the asymptotics
    def some_intermediate_computations_1(self):
        pass
    def some_intermediate_computations_2(self):
        pass
    def some_intermediate_computations_3(self):
        pass

    ...

At Sage Days 28 held this week in Orsay, France, I gave a talk on How to contribute to Sage.

• How to contribute to Sage

The talk goes into the details because we wanted people to contribute during the talk. Tickets created during the talk are here :

• Sage Days 28 trac tickets

The purpose of this text also available on the Sage wiki is to explain how to share your branch of Sage development. I am sure there more than one way to do so, but the solution shown here is the same as the way Sage Combinat shares its development.

First, clone the sage-main. Below, I use my sage trac username to name that branch, because it's my branch of Sage development:

sage -b main
sage -clone slabbe

Go to the directory associated to that new branch and initialize the Queue for Mercurial. See Sage Development Manual : Mercurial queues for more details.

cd SAGE_HOME/devel/sage-slabbe
hg qinit

This last step created a new directory (SAGE_HOME/devel/sage-slabbe/.hg/patches) where your patches will be saved. In order to share your branch, you simply need to share this directory. For example, you can copy its content to a public directory on your web site. You can also use svn, git or any other revision control system. As I want to work on my branch the exact same way as I am working on the sage-combinat branch, I choose to use hg.

Now I log on the server that will host my patches, I create the (public) patches directory and I initialize that directory as an hg directory:

ssh username@server.com
mkdir patches
cd patches
hg init

I also add a hook to that public repository so that it updates itself automatically when a push is made to it. In other words, I edit the file ~/patches/.hg/hgrc so that it becomes:

#file ~/patches/.hg/hgrc
[hooks]
changegroup = hg update

I then logout from the server and go to the patches directory on my machine and make a clone of the public patches repository created above. I could use the http adress, but I use the ssh one so that I can push to the server later on:

cd SAGE_HOME/devel/sage-slabbe/.hg/patches
hg clone ssh://username@server.com:~/patches .

Like for the Sage-combinat repository, I create in .hg/patches a file called .hgignore containing the following:

# file .hgignore
syntax: glob
status
guards

Then, add, commit and push this first change to the server:

hg add .hgignore
hg commit -m "Added the .hgignore file"
hg push

I can now create patches on my branch like in sage-combinat:

cd SAGE_HOME/devel/sage-slabbe/
hg qnew trac_XXXX-fixing-stuff.patch
vim sage/combinat/partition.py
hg qrefresh -e

I can push my changes to my public server like in sage-combinat:

cd SAGE_HOME/devel/sage-slabbe/.hg/patches
hg st
hg commit
hg push

For the first time, you may need to add the series file as well:

cd SAGE_HOME/devel/sage-slabbe/.hg/patches
hg add series
hg commit
hg push

Last thing, notice that the sage-combinat script can be used to install your branch on any Sage installation with the following one liner:

sage -combinat install -b slabbe -s http://server.com/path/to/your/username/patches/

In my case, the result is here

A Fibonacci Tile appearing in the fully packed loop diagram of the permutation \([16,15,13,12,19,22,9,23,26,8,6,29,30,5,31,32,1,2,28,3,4,27,25,7,10,24,11,14,21,20,18,17]\).

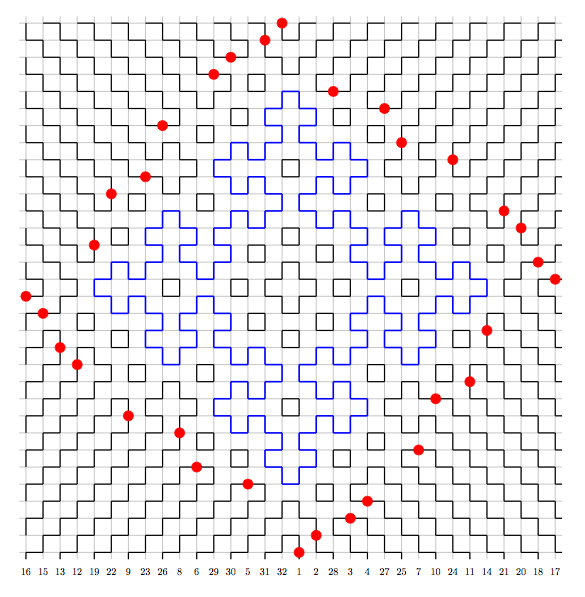
Done with Franco Saliola.

A tamer wants to escape within a circle without being eaten by a lion who lives on the circle. The speed of the lion is 4 times that of the tamer. How can the tamer escape? There is a nice and clever solution in 2d, but does the naive solution where the tamer always moves oppositely to the lion works? In November 2009, a small script written in Sage by Xavier Provençal and Sébastien Labbé in Montpellier answers the question. To create the animation, download the script tamer.sage and run the commands:

sage: load tamer.sage
sage: l = range(0,1200,10)
sage: a = anime(l)
sage: a
Animation with 120 frames
sage: show(a)

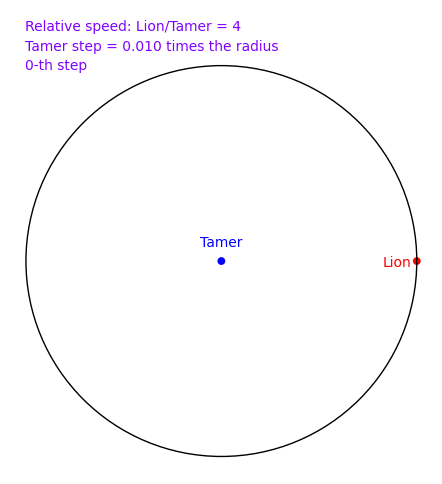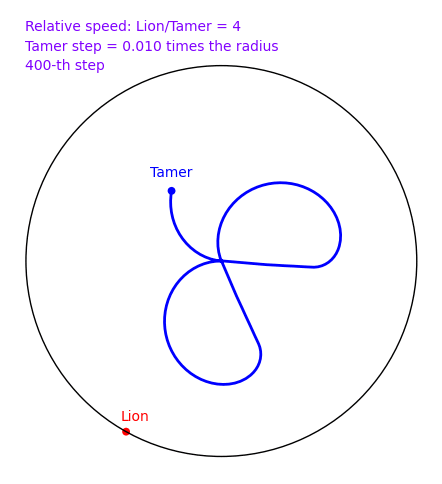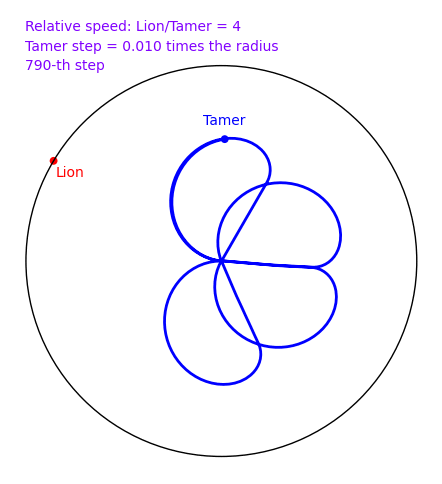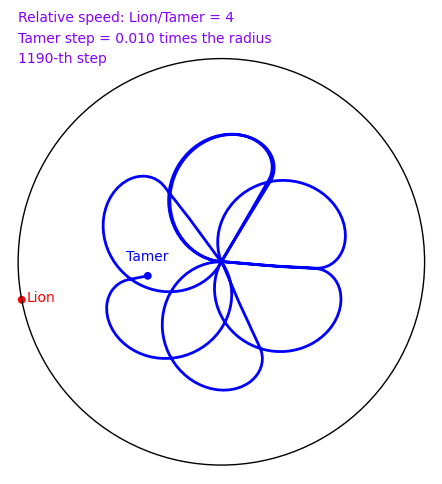
How can the tamer escape? Can you find the solution?