My implementation of André's Joyal Bijection using Sage
12 mai 2012 | Catégories: sage | View CommentsDoron Zeilbeger made a talk last Friday at CRM in Montreal during Sage Days 38 about \(n^{n-2}\). At the end of the talk, he propoed a contest to code Joyal's Bijection which relates double rooted trees on \(n\) vertices and endofunctions on \(n\) elements. I wrote an implementation in Sage. My code is available here : joyal_bijection.sage. It will certainly not win for the most brief code, but it is object oriented, documented, reusable, testable and allows introspection.
Example
First, we must load the file:
sage: load joyal_bijection.sage
Creation of an endofunction:
sage: L = [7, 0, 6, 1, 4, 7, 2, 1, 5] sage: f = Endofunction(L) sage: f Endofunction: [0..8] -> [7, 0, 6, 1, 4, 7, 2, 1, 5]
Creation of a double rooted tree:
sage: L = [(0,6),(2,1),(3,1),(4,2),(5,7),(6,4),(7,0),(8,5)] sage: D = DoubleRootedTree(L, 1, 7) sage: D Double rooted tree: Edges: [(0, 6), (2, 1), (3, 1), (4, 2), (5, 7), (6, 4), (7, 0), (8, 5)] RootA: 1 RootB: 7
From the endofunction f, we get a double rooted tree:
sage: f.to_double_rooted_tree() Double rooted tree: Edges: [(0, 6), (2, 1), (3, 1), (4, 2), (5, 7), (6, 4), (7, 0), (8, 5)] RootA: 1 RootB: 7
From the double rooted tree D, we get an endofunction:
sage: D.to_endofunction() Endofunction: [0..8] -> [7, 0, 6, 1, 4, 7, 2, 1, 5]
In fact, we get D from f and vice versa:
sage: D == f.to_double_rooted_tree() True sage: f == D.to_endofunction() True
Timing
On my machine, it takes 2.23 seconds to transform a random endofunction on \(\{0, 1, \cdots, 9999\}\) to a double rooted tree and then back to the endofunction and make sure the result is OK:
sage: E = Endofunctions(10000) sage: f = E.random_element() sage: time f == f.to_double_rooted_tree().to_endofunction() True Time: CPU 2.23 s, Wall: 2.24 s
Comments
I am using the Sage graph library (Networkx) to find the cycles of a graph and to find the shortest path between two vertices. It would be interesting to compare the timing when using the zen library which is lot faster then networkx.
Testing the IPython 0.12 Notebook
08 mai 2012 | Catégories: sage | View CommentsOn December 21 2011, version 0.12 of IPython was released with its own notebook. The differences with the Sage Notebook are explained by Fernando Perez, leader of IPython project, in the blog post The IPython notebook: a historical retrospective he wrote last January. One of the differences is that the IPython Notebook run in its own directory whereas each cell of the Sage Notebook lives in its directory.
The latest version of IPython is 0.12.1 and was released in April 2012 and I was curious of testing it. I followed the installations informations. I got into trouble some times but finally managed to install it. Below is how I did to install IPython 0.12.1 on my OSX 10.5.8 using Python 2.6.7.
Installing dependencies:
sudo easy_install-2.6 tornado sudo easy_install-2.6 nose sudo easy_install-2.6 pyzmq
The following command was broken for a while:
sudo easy_install-2.6 pyzmq
ending with error TypeError: 'NoneType' object is not callable. I managed to make it work by redoing the above install commands in the correct above order:
sudo easy_install-2.6 tornado sudo easy_install-2.6 nose sudo easy_install-2.6 pyzmq
Installing ipython-0.12:
sudo easy_install-2.6 ipython
To make ipython known from the command line, I added the following line to the file ~/.bash_profile:
# ipython export PATH=/opt/local/Library/Frameworks/Python.framework/Versions/2.6/bin:$PATH
I tested the ipython installation with the iptest command. It finishes with Status: OK
iptest
I open the ipython notebook and it worked:
ipython notebook [NotebookApp] Using existing profile dir: u'/Users/slabbe/.ipython/profile_default' [NotebookApp] The IPython Notebook is running at: http://127.0.0.1:8888 [NotebookApp] Use Control-C to stop this server and shut down all kernels.
In safari, I get the following problem:
Websocket connection to ws://127.0.0.1:8888/kernels/86fef706-f386-4116-b3e4-d6d7776afb0d could not be established. You will NOT be able to run code. Your browser may not be compatible with the websocket version in the server, or if the url does not look right, there could be an error in the server's configuration.
But, in firefox, it works when I open a page at the above adress http://127.0.0.1:8888. It gives me the following dashboard page.
I created my first notebook and did some tests. I followed the documentation found here.
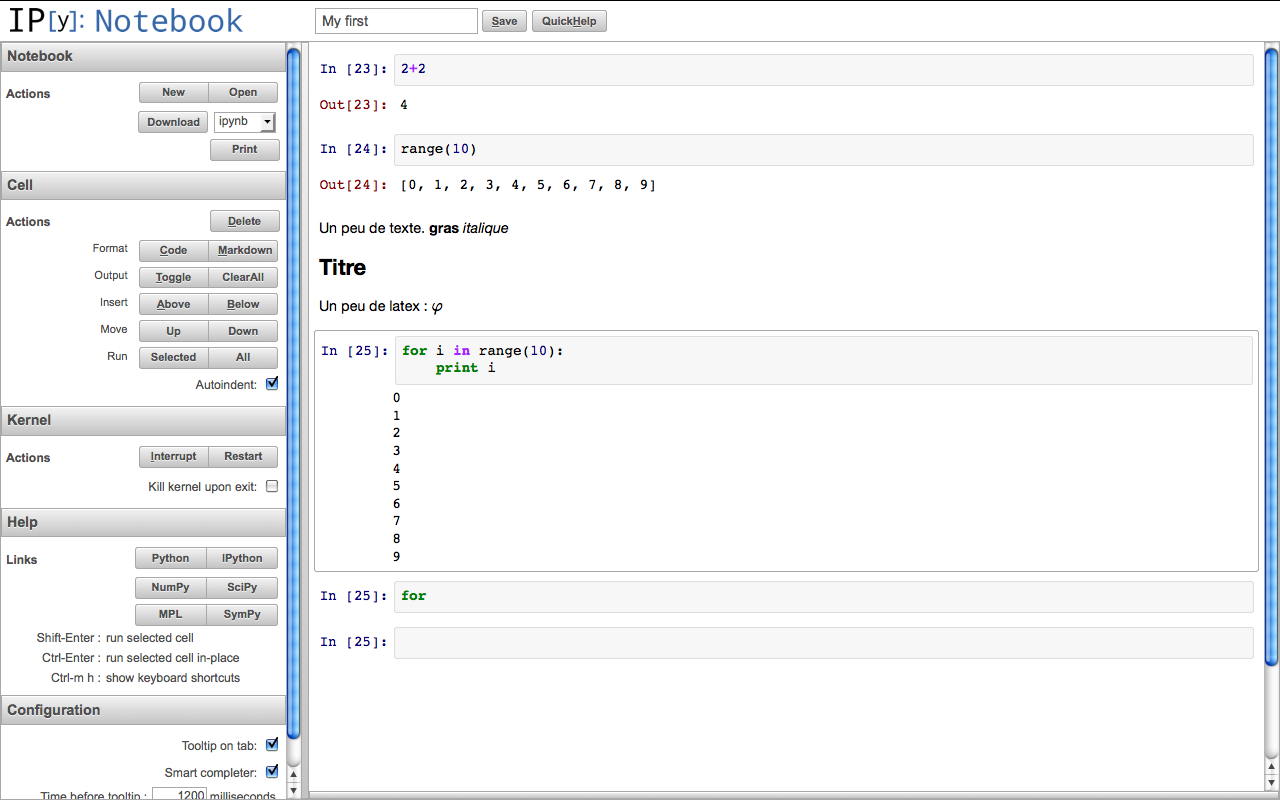
The next thing would be to try to use this with Sage. Some progress has been done and can be followed at ticket #12719.
Evolution of the overall doctest coverage of Sage up to 4.8
01 mai 2012 | Catégories: sage | View CommentsRecently, a discussion on sage-devel mentionned the graph I did last year for the evolution of the overall doctest coverage of Sage. The graph was out of date, so I updated it with the recent data:
Sage 4.7: May 26, 2011 85.4% ~ 23769 / 27833 Sage 4.7.1: August 16, 2011 85.7% ~ 24129 / 28155 Sage 4.7.2: November 03, 2011 86.0% ~ 24477 / 28462 Sage 4.8: January 20, 2012 86.1% ~ 24601 / 28573
We are far from the +4.7% a year I was expecting...
Doctest coverage of Sage
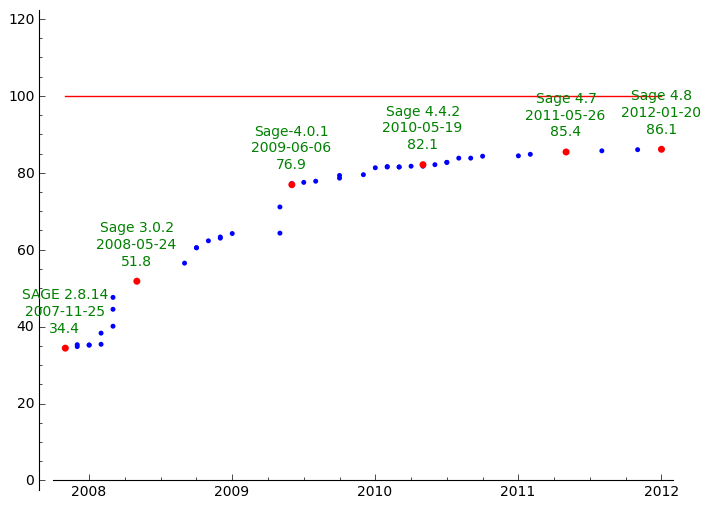
I think we should now stop looking at this percentage for the 100% coverage goal, because the coverage is mostly influenced by the hundreds of new doctested functions that are added to every new version of Sage.
Instead we should consider the evolution of the number of undoctested functions (and maybe fix objectives about it):
Sage 4.7: May 26, 2011 4064 Sage 4.7.1: August 16, 2011 4026 -> 38 old functions now 100% doctested Sage 4.7.2: November 03, 2011 3985 -> 41 old functions now 100% doctested Sage 4.8: January 20, 2012 3972 -> 13 old functions now 100% doctested
Here is the graph of it:
Number of undoctested functions in Sage
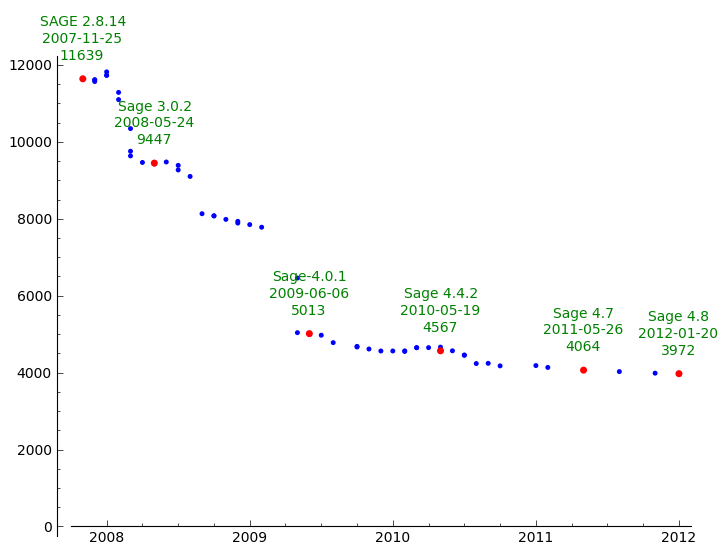
Présentation sur Sage au Cégep de Saint-Hyacinthe
19 janvier 2012 | Catégories: sage | View CommentsAujourd'hui, j'ai fait une présentation sur Sage au département de mathématiques du Cégep de Saint-Hyacinthe. Voici quelques liens.
La présentation (pdf) :
Démo:
Les fichiers txt ci-bas peuvent être chargés à partir du bloc-note (Notebook) de Sage. Copier l'adresse et coller celle-ci dans la page Upload du bloc-note.
Exercices :
- Se créer un compte sur sagenb.org ou sur le serveur du LaCIM.
- Faire un calcul de votre choix.
- Trouver et tester un exemple de votre choix dans le tutoriel en français.
- Trouver et tester un exemple de votre choix dans le wiki de Sage. Recherchez les liens Teaching with Sage, Interact ou Animation.
- Importer (à partir de la page Upload) les feuilles de travail de démonstration ci-haut.
- Consulter les feuilles de travail Sage publiées sur le serveur du LaCIM. Consulter celles indiquant MAT1112 - Chapitre 1 et MAT1112 - Chapitre 2. Je les ai créées à l'automne 2011 pour le cours de Calcul 1 que j'ai donné.
Livre :
- Le livre Calcul mathématique avec Sage. La nouvelle version, sortie en décembre 2011, comporte une centaine de pages de plus que la version précédente. C'est, sans contredit, la meilleure ressource sur Sage en français.
Faire une animation en 3D avec Sage
18 janvier 2012 | Catégories: animation, sage | View CommentsEn Sage, il est relativement facile de créer des animations d'images en 2D. Pour cela, il suffit d'utiliser la commande animate qui s'occupera d'utiliser les commandes plus compliquées ffpmeg ou convert. Plusieurs exemples sont disponibles dans la documentation de Sage ou sur le wiki de Sage.
Par contre, il n'est pas encore possible de faire une animation d'objets graphiques 3D. Le logiciel Jmol, utilisé dans Sage pour faire de la visualisation 3D le permet, car les chimistes l'utilise pour faire des animations 3D de molécules complexes, mais cette fonctionalité n'a pas encore été exportée dans Sage. En juin dernier, j'en ai parlé à Jonathan Gutow, responsable des mises à jour de Jmol dans Sage, mais il doit d'abord régler d'autres problèmes plus importants.
En attendant, il est possible de s'en sortir en utilisant Tachyon plutôt que Jmol. Je rappelle que Tachyon est utilisé dans Sage pour créer des images png d'objets graphiques 3d. Ensuite, on peut immiter ce que la fonction animate fait pour créer une animation d'une scène 3d.
Pour illustrer la méthode par un exemple, faisons une animation de la technique des liens dansants de Knuth pour trouver les solutions du puzzle Quantumino.
Dans un répertoire, créer un fichier Sage video_quantumino.sage qui contiendra le code suivant:
from sage.games.quantumino import QuantuminoSolver import itertools def animate(block=4, stop=400, angle=pi/200.0, nb_pareil=5): r""" This functions creates plenty of png images in the images folder. INPUT: - ``block`` - integer between 0 and 16, the block to put aside - ``stop`` - integer, number of iterations - ``angle`` - number, rotation angle (radian) between each frame - ``nb_parei`` - integer, number of frame per iteration OUTPUT: Plenty of png images in the images folder. """ q = QuantuminoSolver(block) it = q.solve(partial='incremental') i = 0 for solution in itertools.islice(it, stop): G = solution.show3d() G += sphere((4,7,1),size=0.1,opacity=0) # hack to stabilize the frame G += sphere((0,7,0),size=0.1,opacity=0) # hack to stabilize the frame #G += sphere((2,4,1),size=10,opacity=0) # pas opaque pantoute for _ in range(nb_pareil): H = G.rotateZ(angle * i) filename = 'images/image%s.png' % i H.save(filename, frame=False, aspect_ratio=1) print "Création du fichier %s" % filename i += 1 animate(4, stop=20, angle=pi/200.0, nb_pareil=5)
Créer les images à l'aide de Sage >= 4.7.2
mkdir images sage video_quantumino.sage
Aller dans le répertoire images et faites ensuite:
cd images ffmpeg -y -f image2 -r 20 -i image%d.png video.mpg
Le résultat est ici (bloc numéro 4 mis de côté, 200 itérations, angle=\(\pi\)/200, 5 images par itérations, total de 1000 images):
« Previous Page -- Next Page »
