slabbe-0.2.spkg released

30 novembre 2015 | Catégories: sage, slabbe spkg | View Comments

These is a summary of the functionalities present in slabbe-0.2.spkg optional Sage package. It works on version 6.8 of Sage but will work best with sage-6.10 (it is using the new code for cartesian_product merged the the betas of sage-6.10). It contains 7 new modules:

finite_word.py

language.py

lyapunov.py

matrix_cocycle.py

mult_cont_frac.pyx

ranking_scale.py

tikz_picture.py

Cheat Sheets

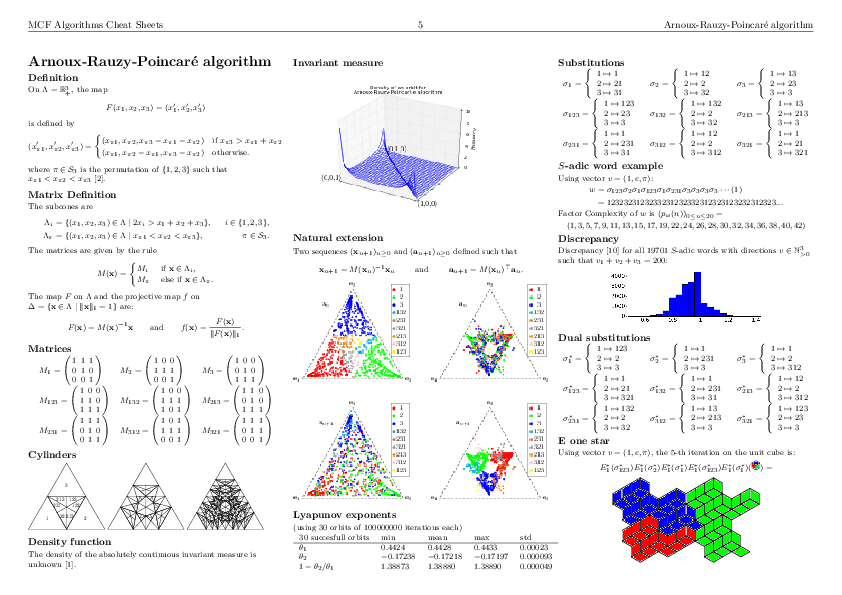
The best way to have a quick look at what can be computed with the optional Sage package slabbe-0.2.spkg is to look at the 3-dimensional Continued Fraction Algorithms Cheat Sheets available on the arXiv since today. It gathers a handful of informations on different 3-dimensional Continued Fraction Algorithms including well-known and old ones (Poincaré, Brun, Selmer, Fully Subtractive) and new ones (Arnoux-Rauzy-Poincaré, Reverse, Cassaigne).

Installation

sage -i http://www.slabbe.org/Sage/slabbe-0.2.spkg    # on sage 6.8
sage -p http://www.slabbe.org/Sage/slabbe-0.2.spkg    # on sage 6.9 or beyond

Examples

Computing the orbit of Brun algorithm on some input in \(\mathbb{R}^3_+\) including dual coordinates:

sage: from slabbe.mult_cont_frac import Brun
sage: algo = Brun()
sage: algo.cone_orbit_list((100, 87, 15), 4)
[(13.0, 87.0, 15.0, 1.0, 2.0, 1.0, 321),
 (13.0, 72.0, 15.0, 1.0, 2.0, 3.0, 132),
 (13.0, 57.0, 15.0, 1.0, 2.0, 5.0, 132),
 (13.0, 42.0, 15.0, 1.0, 2.0, 7.0, 132)]

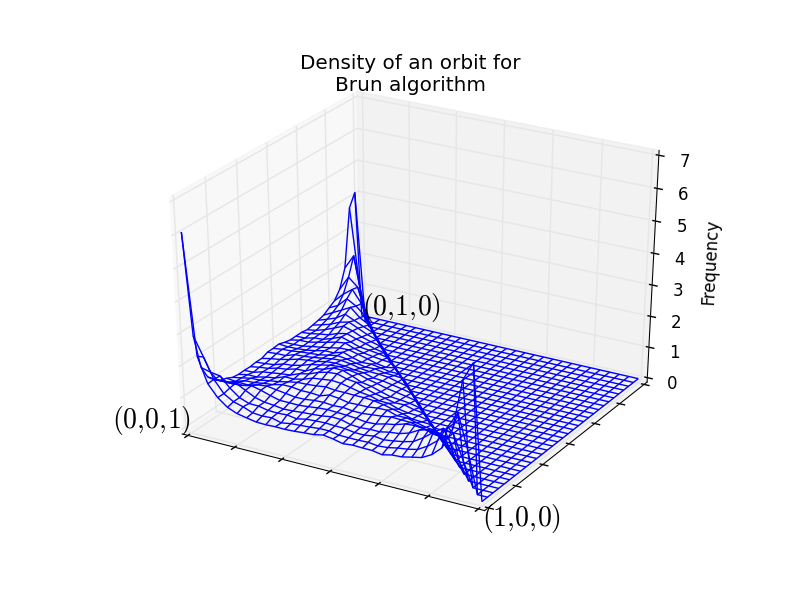
Computing the invariant measure:

sage: fig = algo.invariant_measure_wireframe_plot(n_iterations=10^6, ndivs=30)
sage: fig.savefig('a.png')

/Files/2015/brun_invm_wireframe_plot.png

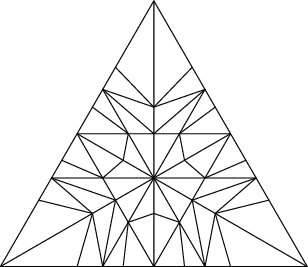
Drawing the cylinders:

sage: cocycle = algo.matrix_cocycle()
sage: t = cocycle.tikz_n_cylinders(3, scale=3)
sage: t.png()

Computing the Lyapunov exponents of the 3-dimensional Brun algorithm:

sage: from slabbe.lyapunov import lyapunov_table
sage: lyapunov_table(algo, n_orbits=30, n_iterations=10^7)
  30 succesful orbits     min       mean      max       std
+-----------------------+---------+---------+---------+---------+
  $\theta_1$              0.3026    0.3045    0.3051    0.00046
  $\theta_2$              -0.1125   -0.1122   -0.1115   0.00020
  $1-\theta_2/\theta_1$   1.3680    1.3684    1.3689    0.00024

Dealing with tikzpictures

Since I create lots of tikzpictures in my code and also because I was unhappy at how the view command of Sage handles them (a tikzpicture is not a math expression to put inside dollar signs), I decided to create a class for tikzpictures. I think this module could be useful in Sage so I will propose its inclusion soon.

I am using the standalone document class which allows some configurations like the border:

sage: from slabbe import TikzPicture
sage: g = graphs.PetersenGraph()
sage: s = latex(g)
sage: t = TikzPicture(s, standalone_configs=["border=4mm"], packages=['tkz-graph'])

The repr method does not print all of the string since it is often very long. Though it shows how many lines are not printed:

sage: t
\documentclass[tikz]{standalone}
\standaloneconfig{border=4mm}
\usepackage{tkz-graph}
\begin{document}
\begin{tikzpicture}
%
\useasboundingbox (0,0) rectangle (5.0cm,5.0cm);
%
\definecolor{cv0}{rgb}{0.0,0.0,0.0}
...
... 68 lines not printed (3748 characters in total) ...
...
\Edge[lw=0.1cm,style={color=cv6v8,},](v6)(v8)
\Edge[lw=0.1cm,style={color=cv6v9,},](v6)(v9)
\Edge[lw=0.1cm,style={color=cv7v9,},](v7)(v9)
%
\end{tikzpicture}
\end{document}

There is a method to generates a pdf and another for generating a png. Both opens the file in a viewer by default unless view=False:

sage: pathtofile = t.png(density=60, view=False)
sage: pathtofile = t.pdf()

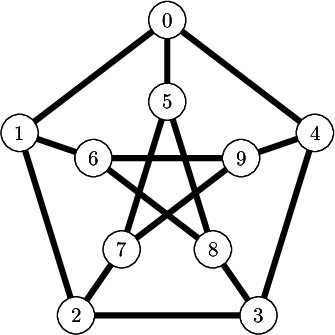
Compare this with the output of view(s, tightpage=True) which does not allow to control the border and also creates a second empty page on some operating system (osx, only one page on ubuntu):

sage: view(s, tightpage=True)

One can also provide the filename where to save the file in which case the file is not open in a viewer:

sage: _ = t.pdf('petersen_graph.pdf')

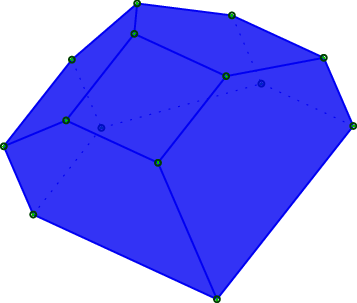
Another example with polyhedron code taken from this Sage thematic tutorial Draw polytopes in LateX using TikZ:

sage: V = [[1,0,1],[1,0,0],[1,1,0],[0,0,-1],[0,1,0],[-1,0,0],[0,1,1],[0,0,1],[0,-1,0]]
sage: P = Polyhedron(vertices=V).polar()
sage: s = P.projection().tikz([674,108,-731],112)
sage: t = TikzPicture(s)
sage: t
\documentclass[tikz]{standalone}
\begin{document}
\begin{tikzpicture}%
        [x={(0.249656cm, -0.577639cm)},
        y={(0.777700cm, -0.358578cm)},
        z={(-0.576936cm, -0.733318cm)},
        scale=2.000000,
...
... 80 lines not printed (4889 characters in total) ...
...
\node[vertex] at (1.00000, 1.00000, -1.00000)     {};
\node[vertex] at (1.00000, 1.00000, 1.00000)     {};
%%
%%
\end{tikzpicture}
\end{document}
sage: _ = t.pdf()

Sébastien Labbé

slabbe-0.2.spkg released