slabbe-0.1.spkg released

27 août 2014 | Catégories: sage, slabbe spkg | View Comments

These is a summary of the functionalities present in slabbe-0.1 optional Sage package. It depends on version 6.3 of Sage because it uses RecursivelyEnumeratedSet code that was merged in 6.3. It contains modules on digital geometry, combinatorics on words and more.

Install the optional spkg (depends on sage-6.3):

sage -i http://www.liafa.univ-paris-diderot.fr/~labbe/Sage/slabbe-0.1.spkg

In each of the example below, you first have to import the module once and for all:

sage: from slabbe import *

To construct the image below, make sure to use tikz package so that view is able to compile tikz code when called:

sage: latex.add_to_preamble("\\usepackage{tikz}")
sage: latex.extra_preamble()
'\\usepackage{tikz}'

Draw the part of a discrete plane

sage: p = DiscretePlane([1,pi,7], 1+pi+7, mu=0)
sage: d = DiscreteTube([-5,5],[-5,5])
sage: I = p & d
sage: I
Intersection of the following objects:
Set of points x in ZZ^3 satisfying: 0 <= (1, pi, 7) . x + 0 < pi + 8
DiscreteTube: Preimage of [-5, 5] x [-5, 5] by a 2 by 3 matrix
sage: clip = d.clip()
sage: tikz = I.tikz(clip=clip)
sage: view(tikz, tightpage=True)

Draw the part of a discrete line

sage: L = DiscreteLine([-2,3], 5)
sage: b = DiscreteBox([0,10], [0,10])
sage: I = L & b
sage: I
Intersection of the following objects:
Set of points x in ZZ^2 satisfying: 0 <= (-2, 3) . x + 0 < 5
[0, 10] x [0, 10]
sage: I.plot()

Double square tiles

This module was developped for the article on the combinatorial properties of double square tiles written with Ariane Garon and Alexandre Blondin Massé [BGL2012]. The original version of the code was written with Alexandre.

sage: D = DoubleSquare((34,21,34,21))
sage: D
Double Square Tile
  w0 = 3032321232303010303230301012101030   w4 = 1210103010121232121012123230323212
  w1 = 323030103032321232303                w5 = 101212321210103010121
  w2 = 2321210121232303232123230301030323   w6 = 0103032303010121010301012123212101
  w3 = 212323032321210121232                w7 = 030101210103032303010
(|w0|, |w1|, |w2|, |w3|) = (34, 21, 34, 21)
(d0, d1, d2, d3)         = (42, 68, 42, 68)
(n0, n1, n2, n3)         = (0, 0, 0, 0)
sage: D.plot()

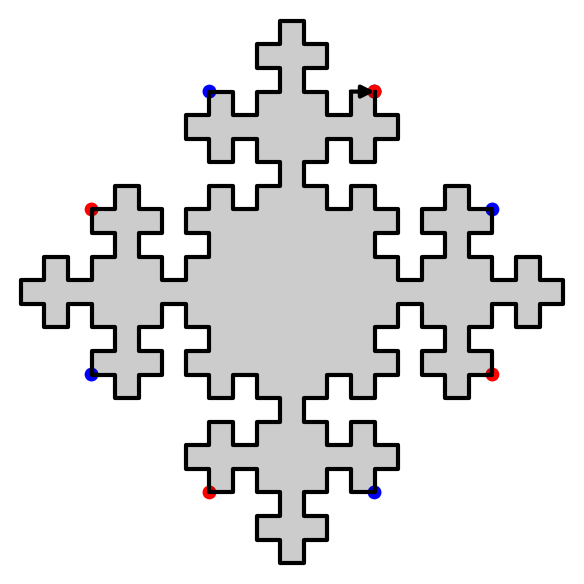
sage: D.extend(0).extend(1).plot()

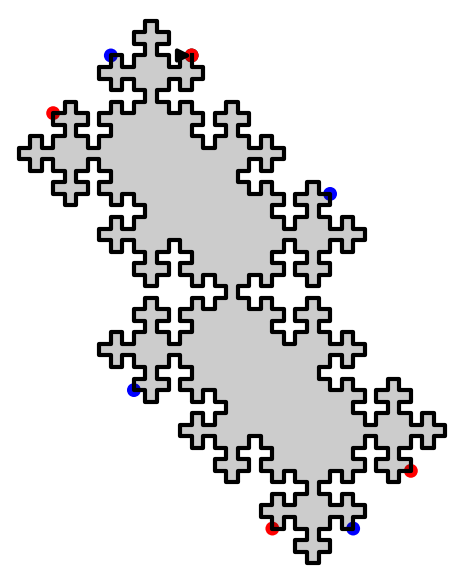
We have shown that using two invertible operations (called SWAP and TRIM), every double square tiles can be reduced to the unit square:

sage: D.plot_reduction()

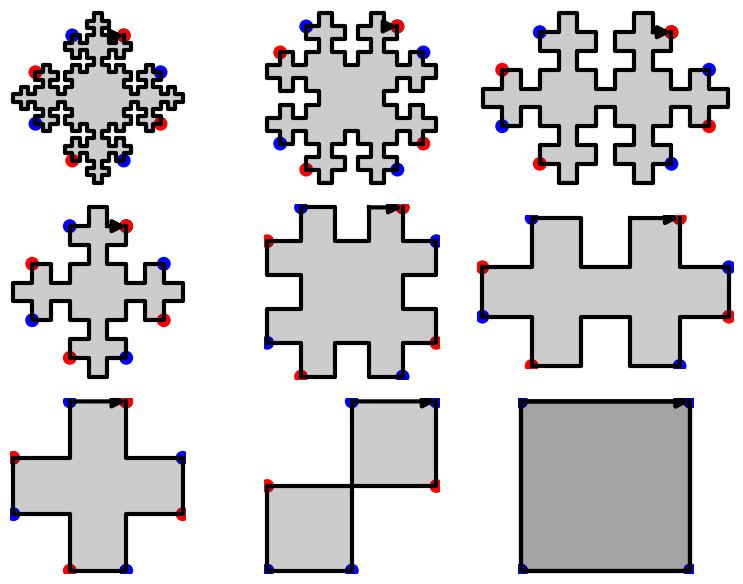
The reduction operations are:

sage: D.reduction()
['SWAP_1', 'TRIM_1', 'TRIM_3', 'SWAP_1', 'TRIM_1', 'TRIM_3', 'TRIM_0', 'TRIM_2']

The result of the reduction is the unit square:

sage: unit_square = D.apply(D.reduction())
sage: unit_square
Double Square Tile
  w0 =     w4 =
  w1 = 3   w5 = 1
  w2 =     w6 =
  w3 = 2   w7 = 0
(|w0|, |w1|, |w2|, |w3|) = (0, 1, 0, 1)
(d0, d1, d2, d3)         = (2, 0, 2, 0)
(n0, n1, n2, n3)         = (0, NaN, 0, NaN)
sage: unit_square.plot()

Since SWAP and TRIM are invertible operations, we can recover every double square from the unit square:

sage: E = unit_square.extend(2).extend(0).extend(3).extend(1).swap(1).extend(3).extend(1).swap(1)
sage: D == E
True

Christoffel graphs

This module was developped for the article on a d-dimensional extension of Christoffel Words written with Christophe Reutenauer [LR2014].

sage: G = ChristoffelGraph((6,10,15))
sage: G
Christoffel set of edges for normal vector v=(6, 10, 15)
sage: tikz = G.tikz_kernel()
sage: view(tikz, tightpage=True)

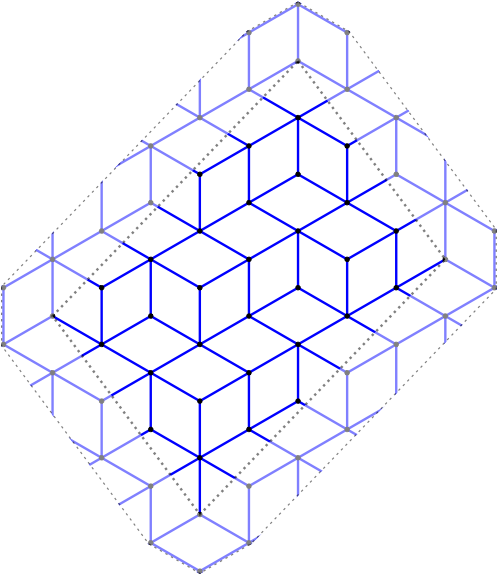
Bispecial extension types

This module was developped for the article on the factor complexity of infinite sequences genereated by substitutions written with Valérie Berthé [BL2014].

The extension type of an ordinary bispecial factor:

sage: L = [(1,3), (2,3), (3,1), (3,2), (3,3)]
sage: E = ExtensionType1to1(L, alphabet=(1,2,3))
sage: E
  E(w)   1   2   3
   1             X
   2             X
   3     X   X   X
 m(w)=0, ordinary
sage: E.is_ordinaire()
True

Creation of a strong-weak pair of bispecial words from a neutral not ordinaire word:

sage: p23 = WordMorphism({1:[1,2,3],2:[2,3],3:[3]})
sage: e = ExtensionType1to1([(1,2),(2,3),(3,1),(3,2),(3,3)], [1,2,3])
sage: e
  E(w)   1   2   3
   1         X
   2             X
   3     X   X   X
 m(w)=0, not ord.
sage: A,B = e.apply(p23)
sage: A
  E(3w)   1   2   3
    1
    2         X   X
    3     X   X   X
 m(w)=1, not ord.
sage: B
  E(23w)   1   2   3
    1          X
    2
    3              X
 m(w)=-1, not ord.

Fast Kolakoski word

This module was written for fun. It uses cython implementation inspired from the 10 lines of C code written by Dominique Bernardi and shared during Sage Days 28 in Orsay, France, in January 2011.

sage: K = KolakoskiWord()
sage: K
word: 1221121221221121122121121221121121221221...
sage: %time K[10^5]
CPU times: user 1.56 ms, sys: 7 µs, total: 1.57 ms
Wall time: 1.57 ms
1
sage: %time K[10^6]
CPU times: user 15.8 ms, sys: 30 µs, total: 15.8 ms
Wall time: 15.9 ms
2
sage: %time K[10^8]
CPU times: user 1.58 s, sys: 2.28 ms, total: 1.58 s
Wall time: 1.59 s
1
sage: %time K[10^9]
CPU times: user 15.8 s, sys: 12.4 ms, total: 15.9 s
Wall time: 15.9 s
1

This is much faster than the Python implementation available in Sage:

sage: K = words.KolakoskiWord()
sage: %time K[10^5]
CPU times: user 779 ms, sys: 25.9 ms, total: 805 ms
Wall time: 802 ms
1

References

[BGL2012]

A. Blondin Massé, A. Garon, S. Labbé, Combinatorial properties of double square tiles, Theoretical Computer Science 502 (2013) 98-117. doi:10.1016/j.tcs.2012.10.040

[LR2014]

Labbé, Sébastien, and Christophe Reutenauer. A d-dimensional Extension of Christoffel Words. arXiv:1404.4021 (April 15, 2014).

[BL2014]

V. Berthé, S. Labbé, Factor Complexity of S-adic sequences generated by the Arnoux-Rauzy-Poincaré Algorithm. arXiv:1404.4189 (April, 2014).

Sébastien Labbé