My status report at Sage Days 57 (RecursivelyEnumeratedSet)

My status report at Sage Days 57 (RecursivelyEnumeratedSet)

11 avril 2014 | Catégories: sage | View Comments

At Sage Days 57, I worked on the trac ticket #6637: standardize the interface to TransitiveIdeal and friends. My patch proposes to replace TransitiveIdeal and SearchForest by a new class called RecursivelyEnumeratedSet that would handle every case.

A set S is called recursively enumerable if there is an algorithm that enumerates the members of S. We consider here the recursively enumerated set that are described by some seeds and a successor function succ. The successor function may have some structure (symmetric, graded, forest) or not. Many kinds of iterators are provided: depth first search, breadth first search or elements of given depth.

TransitiveIdeal and TransitiveIdealGraded

Consider the permutations of \(\{1,2,3\}\) and the poset generated by the method permutohedron_succ:

sage: P = Permutations(3)
sage: d = {p:p.permutohedron_succ() for p in P}
sage: S = Poset(d)
sage: S.plot()
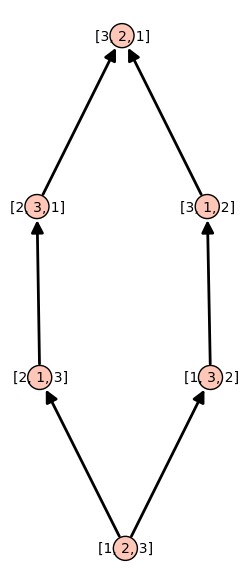
/Files/2014/poset_123.png

The TransitiveIdeal allows to generates all permutations from the identity permutation using the method permutohedron_succ as successor function:

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1,2,3])]
sage: T = TransitiveIdeal(succ, seed)
sage: list(T)
[[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 2, 1], [3, 1, 2]]

Remark that the previous ordering is neither breadth first neither depth first. It is a naive search because it stores the element to process in a set instead of a queue or a stack.

Note that the method permutohedron_succ produces a graded poset. Therefore, one may use the TransitiveIdealGraded class instead:

sage: T = TransitiveIdealGraded(succ, seed)
sage: list(T)
[[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

For TransitiveIdealGraded, the enumeration is breadth first search. Althougth, if you look at the code (version Sage 6.1.1 or earlier), we see that this iterator do not make use of the graded hypothesis at all because the known set remembers every generated elements:

current_level = self._generators
known = set(current_level)
depth = 0
while len(current_level) > 0 and depth <= self._max_depth:
    next_level = set()
    for x in current_level:
        yield x
        for y in self._succ(x):
            if y == None or y in known:
                continue
            next_level.add(y)
            known.add(y)
    current_level = next_level
    depth += 1
return

Timings for TransitiveIdeal

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: T = TransitiveIdeal(succ, seed)
sage: %time L = list(T)
CPU times: user 26.6 ms, sys: 1.57 ms, total: 28.2 ms
Wall time: 28.5 ms

sage: seed = [Permutation([1..8])]
sage: T = TransitiveIdeal(succ, seed)
sage: %time L = list(T)
CPU times: user 14.4 s, sys: 141 ms, total: 14.5 s
Wall time: 14.8 s

Timings for TransitiveIdealGraded

sage: seed = [Permutation([1..5])]
sage: T = TransitiveIdealGraded(succ, seed)
sage: %time L = list(T)
CPU times: user 25.3 ms, sys: 1.04 ms, total: 26.4 ms
Wall time: 27.4 ms

sage: seed = [Permutation([1..8])]
sage: T = TransitiveIdealGraded(succ, seed)
sage: %time L = list(T)
CPU times: user 14.5 s, sys: 85.8 ms, total: 14.5 s
Wall time: 14.7 s

In conlusion, use TransitiveIdeal for naive search algorithm and use TransitiveIdealGraded for breadth search algorithm. Both class do not use the graded hypothesis.

Recursively enumerated set with a graded structure

The new class RecursivelyEnumeratedSet provides all iterators for each case. The example below are for the graded case.

Depth first search iterator:

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: it_depth = R.depth_first_search_iterator()
sage: [next(it_depth) for _ in range(5)]
[[1, 2, 3, 4, 5],
 [1, 2, 3, 5, 4],
 [1, 2, 5, 3, 4],
 [1, 2, 5, 4, 3],
 [1, 5, 2, 4, 3]]

Breadth first search iterator:

sage: it_breadth = R.breadth_first_search_iterator()
sage: [next(it_breadth) for _ in range(5)]
[[1, 2, 3, 4, 5],
 [1, 3, 2, 4, 5],
 [1, 2, 4, 3, 5],
 [2, 1, 3, 4, 5],
 [1, 2, 3, 5, 4]]

Elements of given depth iterator:

sage: list(R.elements_of_depth_iterator(9))
[[5, 4, 2, 3, 1], [4, 5, 3, 2, 1], [5, 3, 4, 2, 1], [5, 4, 3, 1, 2]]
sage: list(R.elements_of_depth_iterator(10))
[[5, 4, 3, 2, 1]]

Levels (a level is a set of elements of the same depth):

sage: R.level(0)
[[1, 2, 3, 4, 5]]
sage: R.level(1)
{[1, 2, 3, 5, 4], [1, 2, 4, 3, 5], [1, 3, 2, 4, 5], [2, 1, 3, 4, 5]}
sage: R.level(2)
{[1, 2, 4, 5, 3],
 [1, 2, 5, 3, 4],
 [1, 3, 2, 5, 4],
 [1, 3, 4, 2, 5],
 [1, 4, 2, 3, 5],
 [2, 1, 3, 5, 4],
 [2, 1, 4, 3, 5],
 [2, 3, 1, 4, 5],
 [3, 1, 2, 4, 5]}
sage: R.level(3)
{[1, 2, 5, 4, 3],
 [1, 3, 4, 5, 2],
 [1, 3, 5, 2, 4],
 [1, 4, 2, 5, 3],
 [1, 4, 3, 2, 5],
 [1, 5, 2, 3, 4],
 [2, 1, 4, 5, 3],
 [2, 1, 5, 3, 4],
 [2, 3, 1, 5, 4],
 [2, 3, 4, 1, 5],
 [2, 4, 1, 3, 5],
 [3, 1, 2, 5, 4],
 [3, 1, 4, 2, 5],
 [3, 2, 1, 4, 5],
 [4, 1, 2, 3, 5]}
sage: R.level(9)
{[4, 5, 3, 2, 1], [5, 3, 4, 2, 1], [5, 4, 2, 3, 1], [5, 4, 3, 1, 2]}
sage: R.level(10)
{[5, 4, 3, 2, 1]}

Recursively enumerated set with a symmetric structure

We construct a recursively enumerated set with symmetric structure and depth first search for default enumeration algorithm:

sage: succ = lambda a: [(a[0]-1,a[1]), (a[0],a[1]-1), (a[0]+1,a[1]), (a[0],a[1]+1)]
sage: seeds = [(0,0)]
sage: C = RecursivelyEnumeratedSet(seeds, succ, structure='symmetric', algorithm='depth')
sage: C
A recursively enumerated set with a symmetric structure (depth first search)

In this case, depth first search is the default algorithm for iteration:

sage: it_depth = iter(C)
sage: [next(it_depth) for _ in range(10)]
[(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 9)]

Breadth first search. This algorithm makes use of the symmetric structure and remembers only the last two levels:

sage: it_breadth = C.breadth_first_search_iterator()
sage: [next(it_breadth) for _ in range(10)]
[(0, 0), (0, 1), (0, -1), (1, 0), (-1, 0), (-1, 1), (-2, 0), (0, 2), (2, 0), (-1, -1)]

Levels (elements of given depth):

sage: sorted(C.level(0))
[(0, 0)]
sage: sorted(C.level(1))
[(-1, 0), (0, -1), (0, 1), (1, 0)]
sage: sorted(C.level(2))
[(-2, 0), (-1, -1), (-1, 1), (0, -2), (0, 2), (1, -1), (1, 1), (2, 0)]

Timings for RecursivelyEnumeratedSet

We get same timings as for TransitiveIdeal but it uses less memory so it might be able to enumerate bigger sets:

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: %time L = list(R)
CPU times: user 24.7 ms, sys: 1.33 ms, total: 26.1 ms
Wall time: 26.4 ms

sage: seed = [Permutation([1..8])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: %time L = list(R)
CPU times: user 14.5 s, sys: 70.2 ms, total: 14.5 s
Wall time: 14.6 s
blog comments powered by Disqus