Sébastien Labbé

On the bifurcation diagram proposed by Jang and Robinson

2025-05-06T14:37:00Z

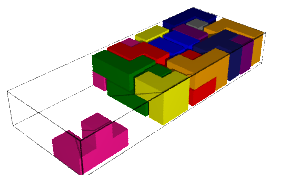
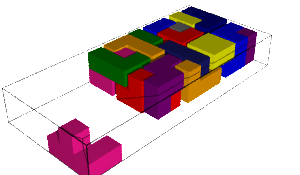
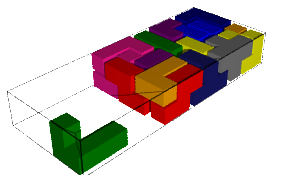
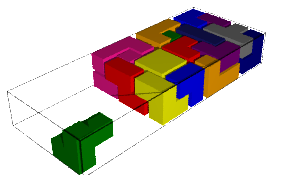
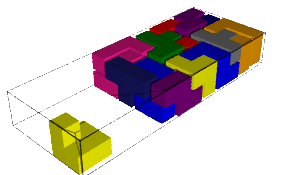
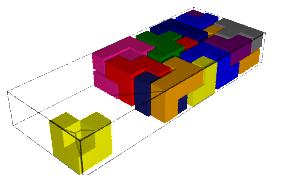
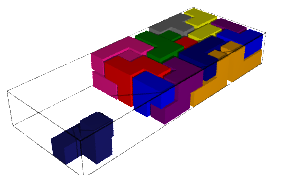
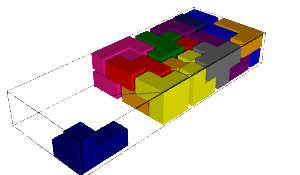
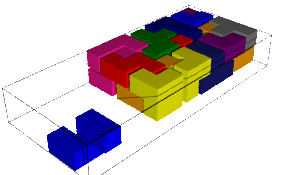
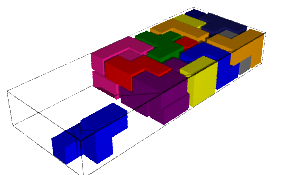
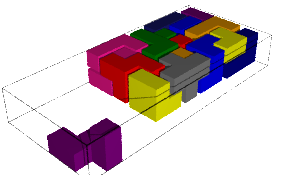
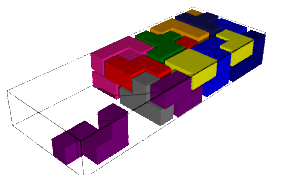
In this blog post, we present a few remarks on the "bifurcation diagram" proposed by Jang and Robinson in [1] to describe the tilings associated to a set of 24 Wang tiles encoding Penrose tilings.

[1] Hyeeun Jang, E. Arthur Robinson Jr, Directional Expansiveness for Rd-Actions and for Penrose Tilings, arxiv:2504.10838

In particular, I believe that something is wrong in what the authors call the "bifurcation diagram" shown in Figure 10. But, as we illustrate below, it can be fixed easily by permuting some of the labels of the partition.

I saw Jang and Robinsion's bifurcation diagram for the first time during the talk "Remembering Shunji Ito" made by Robinson during the online conference dedicated to the memory of Shunji Ito on December 14, 2021. At that time, I was working on the family of metallic mean Wang tiles. This is why the bifurcation diagram shown by Robinson and extracted from Jang's PhD thesis got my attention right away, because it was looking very much like the Markov partition associated to the Ammann set of 16 Wang tiles, the first member of the family of metallic mean Wang tiles. As we illustrate below, Jang and Robinson's bifurcation diagram is a refinement of the Markov partition associated the Ammann set of 16 Wang tiles. This means that the 16 tiles Ammann Wang shift is a factor of the 24 tiles Penrose Wang shift. Also most probably the bifurcation diagram is a Markov Partition for the same associated toral ℤ²-action. But this needs a proof.

The content of this blog post is also available as a Jupyter notebook that can be viewed and downloaded from the nbviewer.

Dependencies

The computations made here depend on the modules WangTileSet, WangTiling, PolyhedronPartition, PolyhedronExchangeTransformation, PETsCoding implemented in the SageMath optional package slabbe over the last years in order to describe and study the Jeandel-Rao aperiodic tilings and the family of metallic mean Wang tiles.

Note that the package slabbe can be installed by running !pip install slabbe directly in SageMath:

sage: # !pip install slabbe             # uncomment and execute this line to install slabbe package

Here are the version of the packages used in this post:

sage: import importlib
sage: importlib.metadata.version("slabbe")
'0.8.0'

sage: version()
'SageMath version 10.5.beta6, Release Date: 2024-09-29'

Jang-Robinson encoding of the Penrose 24 Wang tiles

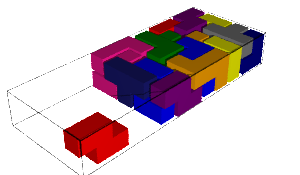
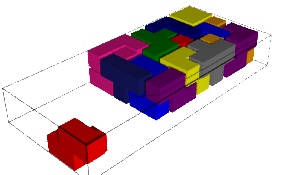
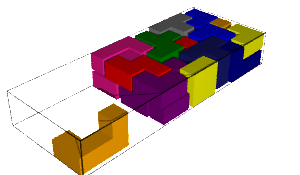
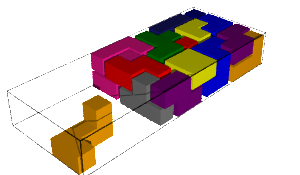
We encode the 24 Wang tiles proposed by Jang and Robinson (Figure 9 of [1]) using alphabet {A, B, C, D, E, F, G, H, I, J} for the shapes:

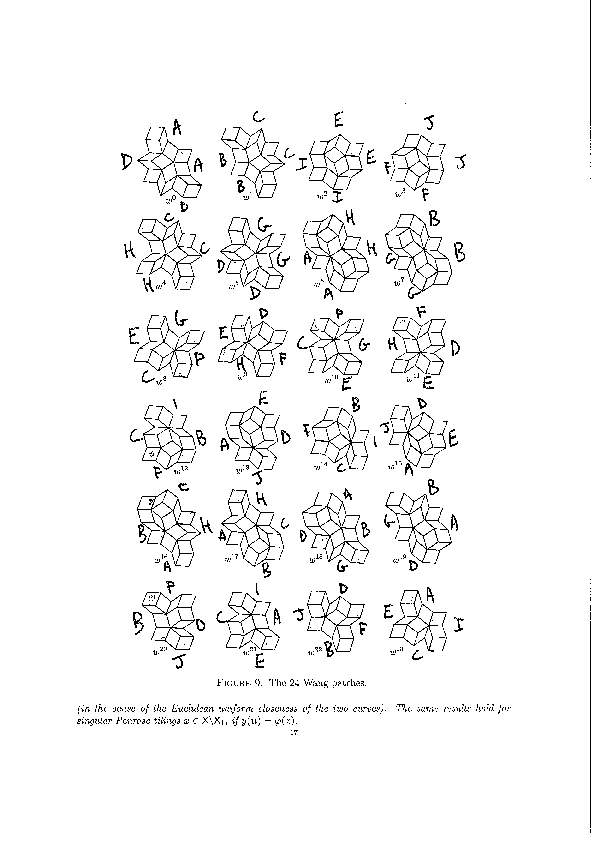
We define the 24 Wang tiles in SageMath:

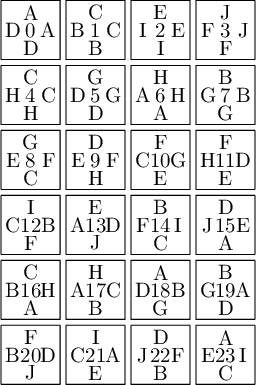
sage: from slabbe import WangTileSet, WangTiling
sage: tiles = ["AADD", "CCBB", "EEII", "JJFF",
....:          "CCHH", "GGDD", "HHAA", "BBGG",
....:          "FGEC", "FDEH", "GFCE", "DFHE",
....:          "BICF", "DEAJ", "IBFC", "EDJA",
....:          "HCBA", "CHAB", "BADG", "ABGD",
....:          "DFBJ", "AICE", "FDJB", "IAEC"]
sage: T0 = WangTileSet([tuple(str(a) for a in tile) for tile in tiles])
sage: T0
Wang tile set of cardinality 24

sage: T0.tikz(ncolumns=4)

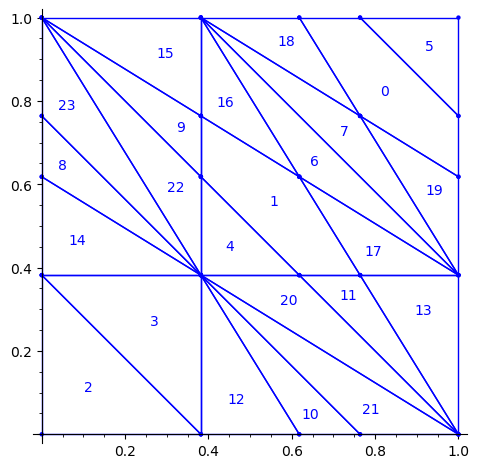
Constructing Jang-Robinson Bifurcation diagram as a polygonal partition

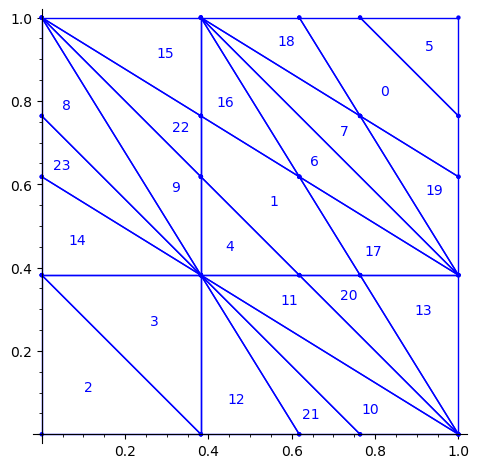
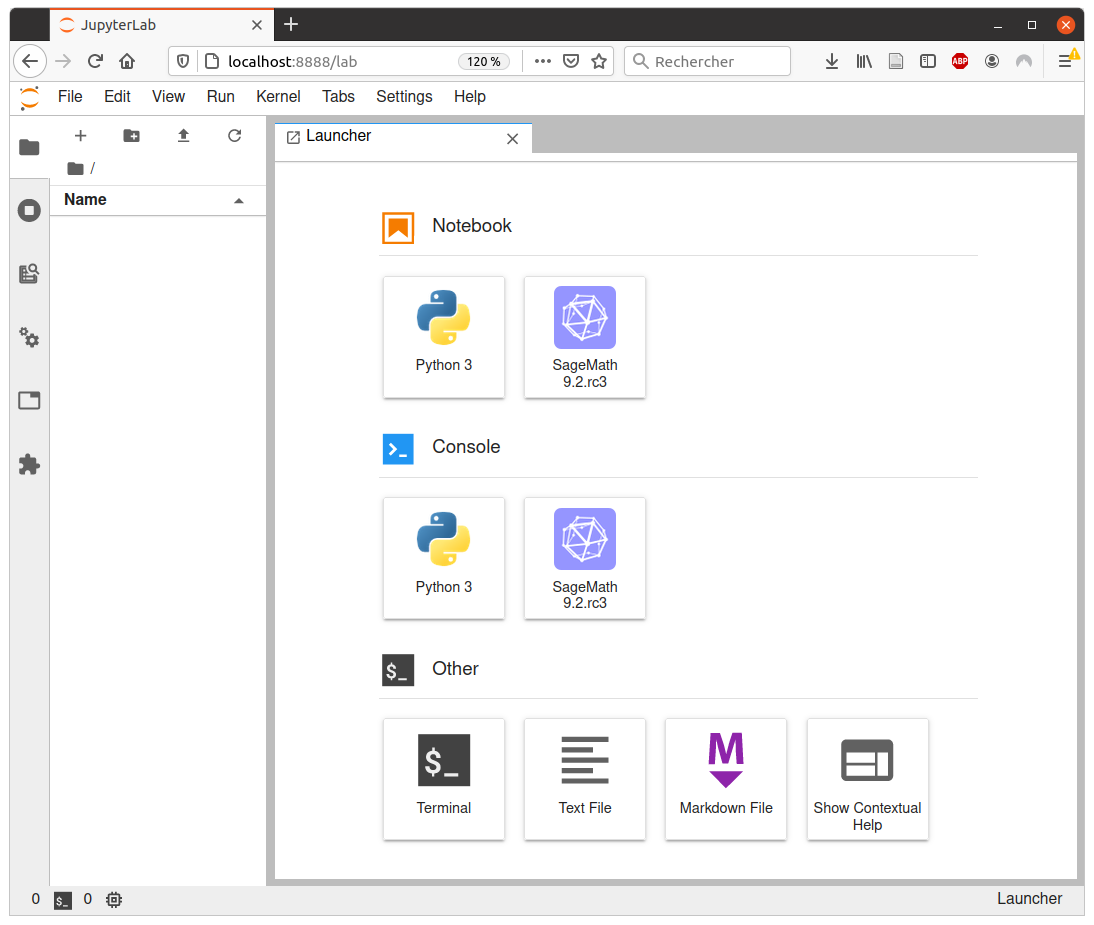
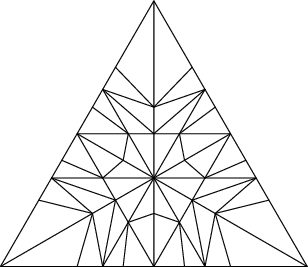
Below is a reproduction of Jang-Robinson bifurcation diagram shown in Figure 10 from arxiv:2504.10838

In this section, we construct this bifurcation diagram in SageMath as a polygonal partition.

sage: from slabbe import PolyhedronPartition

sage: z = polygen(QQ, 'z')
sage: K = NumberField(z**2-z-1, 'phi', embedding=RR(1.6))
sage: phi = K.gen()

sage: square = polytopes.hypercube(2,intervals = 'zero_one')
sage: P = PolyhedronPartition([square])
sage: P = P.refine_by_hyperplane([1/phi^3,-1,-1])
sage: P = P.refine_by_hyperplane([1/phi,-1,-1])
sage: P = P.refine_by_hyperplane([1,-1,-1])
sage: P = P.refine_by_hyperplane([1 + 1/phi,-1,-1])
sage: P = P.refine_by_hyperplane([1 + 1/phi^3,-1,-1])
sage: P = P.refine_by_hyperplane([1/phi,-phi,-1])
sage: P = P.refine_by_hyperplane([1,-phi,-1])
sage: P = P.refine_by_hyperplane([phi,-phi,-1])
sage: P = P.refine_by_hyperplane([1/phi^2,-1/phi,-1])
sage: P = P.refine_by_hyperplane([1/phi,-1/phi,-1])
sage: P = P.refine_by_hyperplane([1,-1/phi,-1])
sage: P = P.refine_by_hyperplane([1/phi,-1,0])
sage: P = P.refine_by_hyperplane([1/phi,0,-1])
sage: P = -P
sage: P = P.translate((1,1))
sage: #P.plot()
sage: P = P.rename_keys({0:5, 1:0, 2:18, 3:19, 4:7, 5:6, 6:16, 7:17, 8:1, 9:4, 10:15,11:9,
sage:                    12:22,13:23,14:8, 15:14,16:13,17:11,18:20,19:21,20:10, 21:12, 22:3,
sage:                    23:2})
sage: P.plot()

Our claim

We claim that the above bifurcation diagram from Jang-Robinson preprint is slightly wrong according to the choice of indices of the 24 Wang tiles made by Jang and Robinson and shown above. The following changes should be made in order to fix the partition:

indices 9 and 22 should be swapped,

indices 8 and 23 should be swapped,

indices 11 and 20 should be swapped and

indices 10 and 21 should be swapped.

Defining the toral translations in the internal space as PETs

We define the toral translations associated to the partition chosen by Jang-Robinson. The internal space is the 2-dimensional torus ℝ² ⁄ ℤ². It is represented as the unit square [0, 1)². On this fundamental domain, a toral translation is a polygon exchange transformation.

Note that according to their choice,

a unit horizontal translation in the physical space corresponds to a vertical translation by (0, φ) in the internal space,

a unit vertical translation in the physical space corresponds to a horizontal translation by (φ, 0) in the internal space,

where φ is the golden mean.

Below, we follow their convention.

sage: from slabbe import PolyhedronExchangeTransformation as PET

sage: base = diagonal_matrix((1,1))
sage: R0e1 = PET.toral_translation(base, vector((0,phi)))
sage: R0e2 = PET.toral_translation(base, vector((phi,0)))

We compute a 10×10 pattern obtained by coding the orbit of some starting point under the ℤ²-action R₀.

sage: from slabbe.coding_of_PETs import PETsCoding

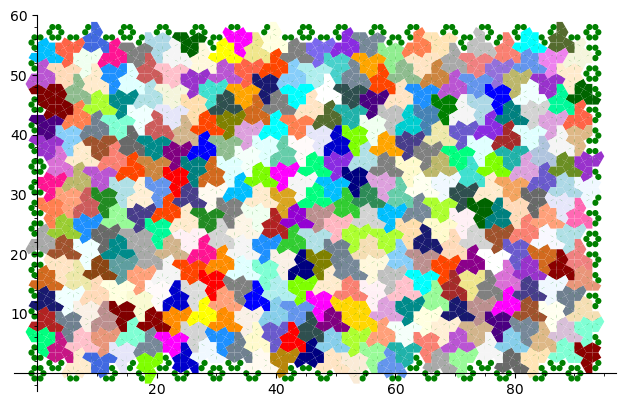
sage: coding_R0_P = PETsCoding((R0e1,R0e2), P)
sage: pattern = coding_R0_P.pattern((.3,.4), (10,10))
sage: pattern = WangTiling(pattern, T0)
sage: pattern.tikz()

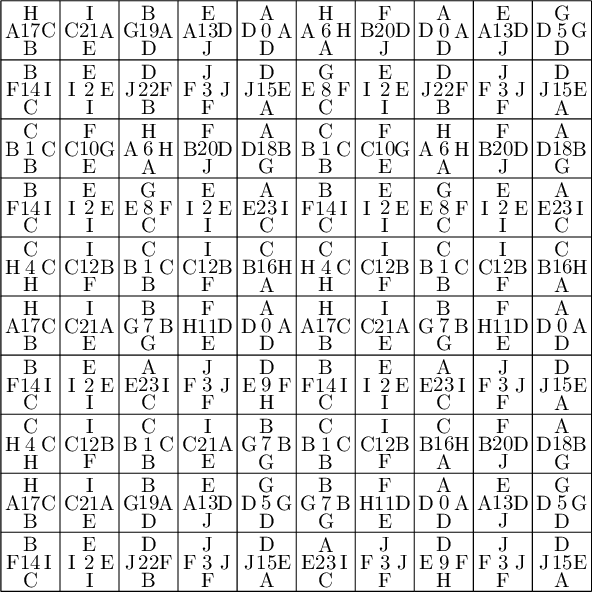
We observe that this pattern is not valid !!!

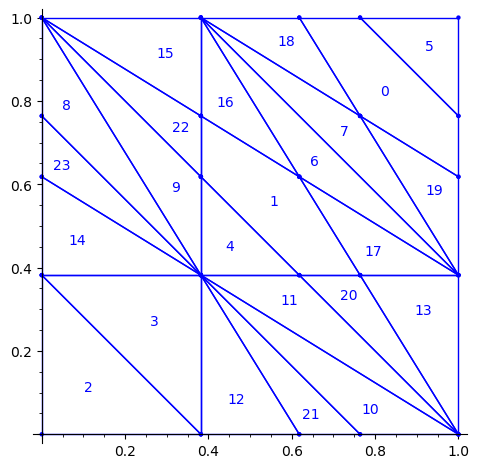
Let's fix the partition

We claim that the above pattern is wrong because something is wrong in the labelling of the atoms in the partition proposed by Jang and Robinson for the 24 Wang tiles encoding Penrose tilings.

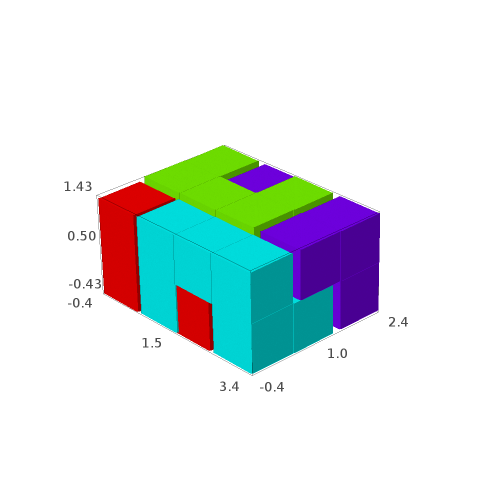
Below, we fix the partition by swapping labels 8 and 23, 9 and 22, 11 and 20, 10 and 21:

sage: d = {i:i for i in range(24)}
sage: d.update({8:23, 23:8, 9:22, 22:9, 11:20, 20:11, 10:21, 21:10})
sage: P1 = P.rename_keys(d)
sage: P1.plot()

We compute a 10×10 pattern out of this updated partition P₁:

sage: coding_R0_P1 = PETsCoding((R0e1,R0e2), P1)
sage: pattern = coding_R0_P1.pattern((.3,.4), (10,10))
sage: pattern = WangTiling(pattern, T0)
sage: pattern.tikz()

We observe that this pattern is valid !!!

Understanding the issue using edge label partitions

Let us try to understand the fix in terms of the Wang tiles east, north, west and south edge labels partitions induced by the original partition.

Indeed, since each atom of the partition corresponds to a Wang tile, we can deduce a partition of the unit square for the east labels (and respectively for the north, west and south labels) by merging two atoms in the partition if their east edge label is the same.

sage: def edge_label_partitions(partition, tiles):
....:     EAST = partition.merge_atoms({i:tiles[i][0] for i in range(24)})
....:     NORTH = partition.merge_atoms({i:tiles[i][1] for i in range(24)})
....:     WEST = partition.merge_atoms({i:tiles[i][2] for i in range(24)})
....:     SOUTH = partition.merge_atoms({i:tiles[i][3] for i in range(24)})
....:     return EAST, NORTH, WEST, SOUTH
sage: def draw_edge_label_partitions(partition, tiles):
....:     EAST, NORTH, WEST, SOUTH = edge_label_partitions(partition, tiles)
....:     L = [EAST.plot() + text('EAST', (.5,1.05)),
....:          NORTH.plot() + text('NORTH', (.5,1.05)),
....:          WEST.plot() + text('WEST', (.5,1.05)),
....:          SOUTH.plot() + text('SOUTH', (.5,1.05))]
....:     return graphics_array(L, nrows=2)

This is what we get using the partition proposed by Jang and Robinson for the 24 Wang tiles encoding Penrose tilings:

sage: draw_edge_label_partitions(P, T0)

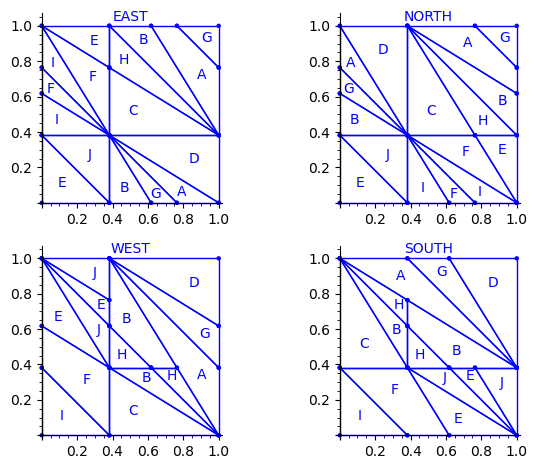
Here are some observations which are normal:

partitions NORTH and EAST are symmetric under a reflexion by the positive diagonal (remember that the tile set is symmetric under the positive diagonal)

partitions WEST and SOUTH are symmetric under a reflexion by the positive diagonal (remember that the tile set is symmetric under the positive diagonal)

Here are some observations which are not normal:

partitions WEST and EAST do not give the same area to the same index (in a Wang tiling, the frequency of a EAST label should be equal to the frequency of the same WEST label)

partitions SOUTH and NORTH do not give the same area to the same index (in a Wang tiling, the frequency of a NORTH label should be equal to the frequency of the same SOUTH label)

partitions EAST and WEST are not a translate of one another (idealy a horizontal translate)

partitions SOUTH and NORTH are not a translate of one another (idealy a vertical translate)

Another indication that something may be wrong is:

atoms B, H, E, J, A, G are not convex in the torus

This is not a necessity. Atoms are not convex in the Markov partition associated to Jeandel-Rao tilings [2]. But they are convex for the Ammann set of 16 Wang tiles and their generalization to metallic mean numbers made in [3,4]. Since Penrose tilings are closely related to Ammann A2 tilings, we may also expect to have simple convex atoms in each of the four edge label partitions.

[2] Markov partitions for toral ℤ2-rotations
featuring Jeandel-Rao Wang shift and model sets, Annales Henri
Lebesgue 4 (2021) 283-324. doi:10.5802/ahl.73
[3] Metallic mean Wang tiles I: self-similarity, aperiodicity and
minimality, arxiv:2312.03652
[4] Metallic mean Wang tiles II: the dynamics of an aperiodic computer
chip, arxiv:2403.03197

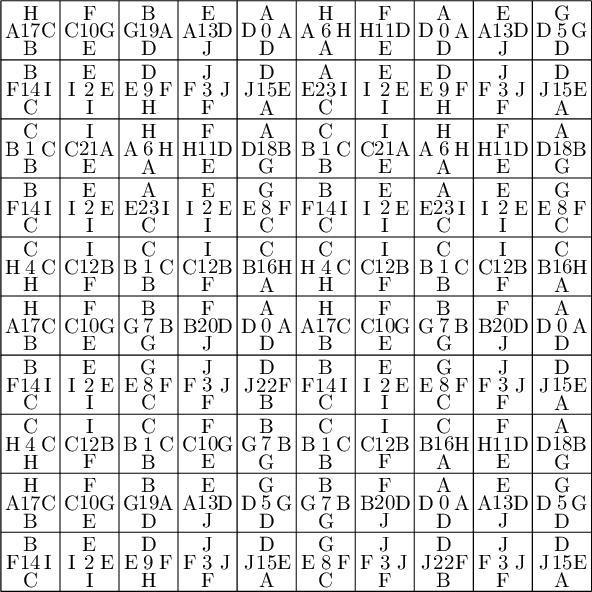
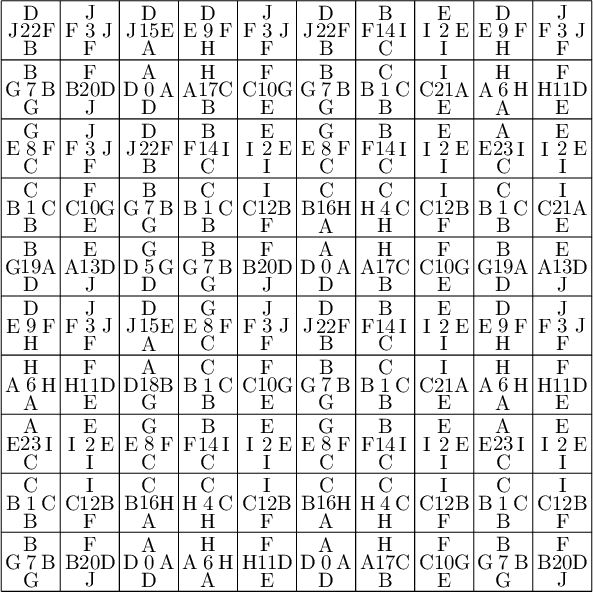
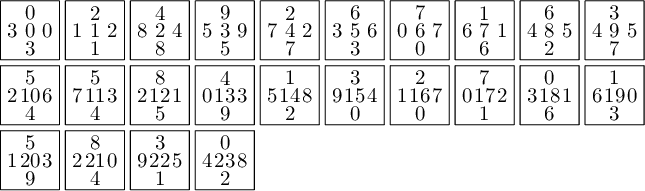
Here is the area of each atom in each of the four partitions. We observe that only atoms C and D have the same area in each of the four partitions.

sage: def table_of_area_of_atom_in_east_north_west_south_partitions(partition, tiles):
....:     columns = []
....:     labels = 'ABCDEFGHIJ'
....:     EAST, NORTH, WEST, SOUTH = edge_label_partitions(partition, tiles)
....:     for partition in [EAST, NORTH, WEST, SOUTH]:
....:         d = partition.volume_dict()
....:         column = [d[a] for a in labels]
....:         columns.append(column)
....:     header_row = ['EAST', 'NORTH', 'WEST', 'SOUTH']
....:     return table(columns=columns, header_row=header_row, header_column=['']+list(labels))

sage: table_of_area_of_atom_in_east_north_west_south_partitions(P, T0)
    │ EAST             NORTH            WEST             SOUTH
├───┼────────────────┼────────────────┼────────────────┼────────────────┤
  A │ 15/2*phi - 12    15/2*phi - 12    phi - 3/2        phi - 3/2
  B │ phi - 3/2        phi - 3/2        15/2*phi - 12    15/2*phi - 12
  C │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  D │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  E │ phi - 3/2        phi - 3/2        -11/2*phi + 9    -11/2*phi + 9
  F │ -11/2*phi + 9    -11/2*phi + 9    phi - 3/2        phi - 3/2
  G │ -8*phi + 13      -8*phi + 13      -3/2*phi + 5/2   -3/2*phi + 5/2
  H │ -3/2*phi + 5/2   -3/2*phi + 5/2   -8*phi + 13      -8*phi + 13
  I │ 5*phi - 8        5*phi - 8        -3/2*phi + 5/2   -3/2*phi + 5/2
  J │ -3/2*phi + 5/2   -3/2*phi + 5/2   5*phi - 8        5*phi - 8

But, we observe that we can fix the partitions if we assume that the atoms C and D in the four partitions are correct. There is a unique translation sending atoms C,D in the partition WEST to the atoms C and D in the partition EAST. That translation should send the partition WEST exactly on EAST. Similarly for SOUTH and NORTH. This suggest a way to fix atoms B, H, E, J, A, G in the partition.

Fixed Edge labels partitions

Using the fixed partition, here is what we get.

sage: P1.plot()

sage: draw_edge_label_partitions(P1, T0)

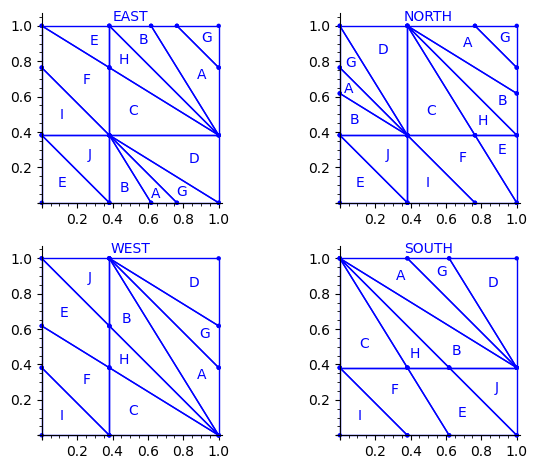
Now it looks good! As for the partitions associated to the metallic mean Wang tiles, the four partitions are isometric copies of the other ones (under toral translation or reflection).

sage: table_of_area_of_atom_in_east_north_west_south_partitions(P1, T0)
    │ EAST             NORTH            WEST             SOUTH
├───┼────────────────┼────────────────┼────────────────┼────────────────┤
  A │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  B │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  C │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  D │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  E │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  F │ phi - 3/2        phi - 3/2        phi - 3/2        phi - 3/2
  G │ -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2
  H │ -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2
  I │ -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2
  J │ -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2   -3/2*phi + 5/2

sage: (phi-3/2).n(), (-3/2*phi + 5/2).n()
(0.118033988749895, 0.0729490168751576)

Labels A, B, C, D, E and F all have the same frequency of ϕ − (3)/(2) ≈ 0.118.

Labels G, H, I and J all have the same frequency of − (3)/(2)ϕ + (5)/(2) ≈ 0.0729.

We check that frequencies sum to 1:

sage: 6 * (phi-3/2) + 4 * (-3/2*phi + 5/2)
1

Proposed partition for the encoding of the Penrose tilings into 24 Wang tiles

As done with the Markov partition associated to Jeandel-Rao aperiodic tilings, and for the Markov partition associated to the family of metallic mean Wang tiles, I think it is more natural to associate horizontal (vertical) translations in the internal space with horizontal (vertical) translations in the physical space. This way, the brain is less mixed up and the projections in the physical space π and in the internal space π_int of the cut and project scheme are defined more naturally. This way the internal space and physical space can even be identified: this is the root of the do-it-yourself tutorial allowing the construction of Jeandel-Rao tilings [5]. See also my Habilitation à diriger des recherches written in English during Spring 2025 for more information [6].

[5] A do-it-yourself polygonal partition to construct Jeandel-Rao tilings, April 2024,

[6] Sébastien Labbé, Aperiodic order: from combinatorics to geometry via symbolic dynamics, number theory and algorithms, Mémoire d’habilitation à diriger des recherches,

First, we flip the partition P₁ by the positive diagonal. This exchanges the role of x and y axis.

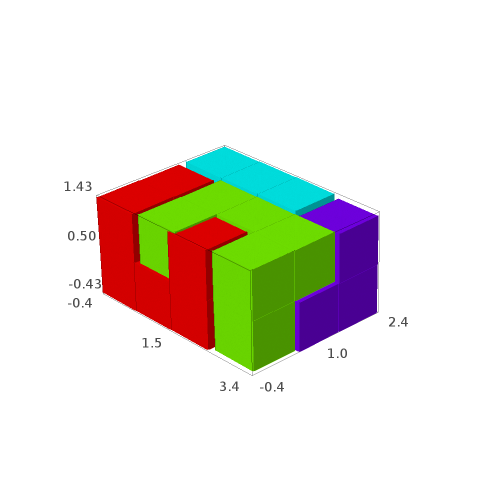
sage: P2 = P1.apply_linear_map(matrix(2, [0,1,1,0]))
sage: P2.plot()

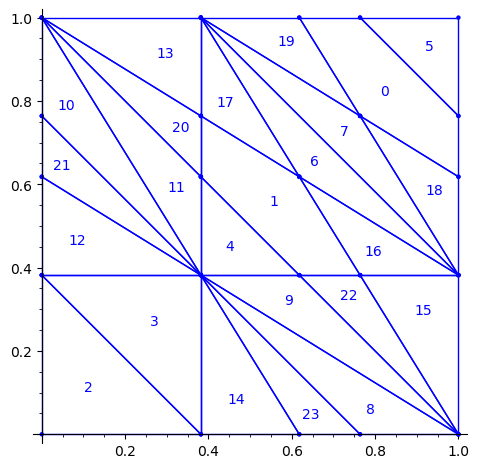
This allows to define the ℤ²-action R₁ on the torus with horizontal and vertical translations for e₁ and e₂ respectively:

sage: base = diagonal_matrix((1,1))
sage: R1e1 = PET.toral_translation(base, vector((1/phi,0)))
sage: R1e2 = PET.toral_translation(base, vector((0,1/phi)))

Then, we rotate the partition. This changes the origin of the partition. This change may be optional, but it makes the partition look closer to the partitions already studied in [2,3,4]. It simplifies the explanation of any relation between them (and there is one, see below!).

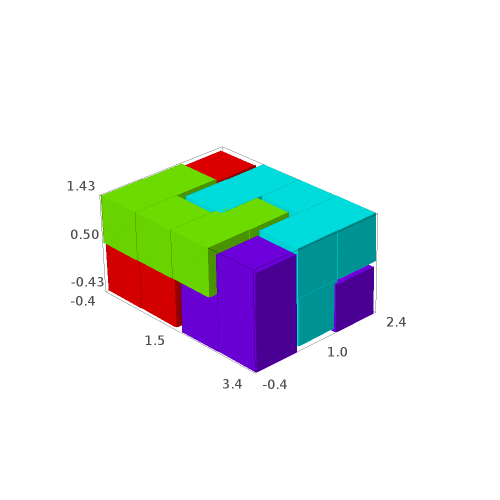
sage: P3 = R1e1(P2)
sage: P3 = R1e2(P3)
sage: P3.plot()

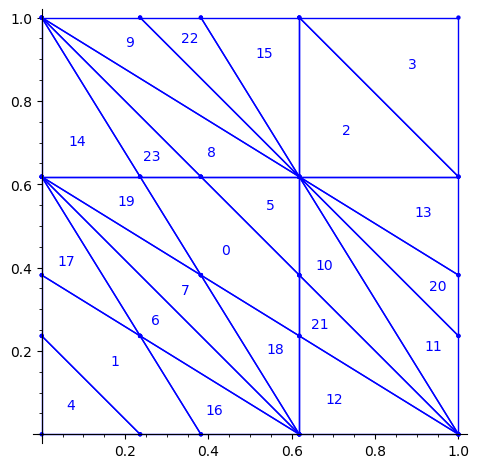
We observe that the partition P₃ associated to the 24 Wang tiles encoding Penrose tiling is a refinement of the partition associated to the 16 Ammann tiles (see Figure 15 in [4] as the 16 Ammann tiles are equivalent to the n-th metallic mean Wang tiles when n = 1).

We compute a 10×10 pattern obtained by coding the orbit of some starting point under the ℤ²-action R₁ using partition P₃.

sage: from slabbe.coding_of_PETs import PETsCoding

sage: coding_R1_P3 = PETsCoding((R1e1,R1e2), P3)
sage: pattern = coding_R1_P3.pattern((.3,.4), (10,10))
sage: pattern = WangTiling(pattern, T0)
sage: pattern.tikz()

We are happy to see that the pattern is still valid after all the changes we have made!

sage: draw_edge_label_partitions(P3, T0)

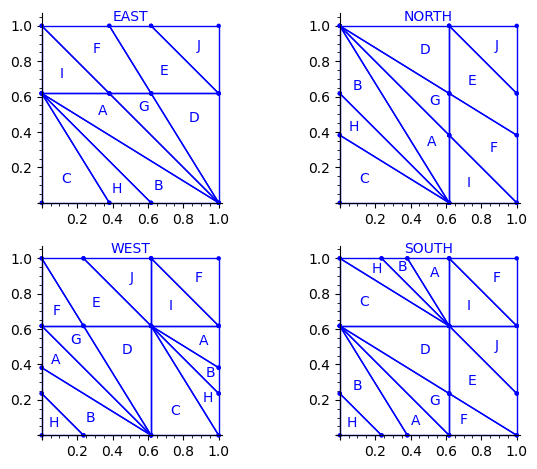
We observe that the EAST, NORTH, WEST and SOUTH partitions are a refinement of the EAST, NORTH, WEST and SOUTH partitions associated to the Ammann tiles partition (see Figure 15 in [4]).

The difference between the Ammann EAST and 24 Wang tiles Penrose EAST partition is the addition of two closed geodesics of slope -1 on the 2-torus passing through the origin and through the vertex (0, φ^− 1).

It is possible that there is a clever way of including this information into the labels of the Wang tiles as we have done it for the family of metallic mean Wang tiles. Possibly, we need to use 4-dimension vectors for the tile labels instead of 3-dimensional integer vectors. This remains an open question.

Wang tiles deduced from the partition and ℤ²-action

We check that the Wang tiles computed from the partition P₃ and ℤ²-action R₁ is the original set of 24 Wang tiles defined by Jang and Robinson.

See Proposition 8.1 in [2].

sage: T = coding_R1_P3.to_wang_tiles()
sage: T.tikz()

sage: T.is_equivalent(T0, certificate=True)
(True,
 {'3': 'D',
  '0': 'A',
  '6': 'G',
  '1': 'B',
  '7': 'H',
  '2': 'C',
  '8': 'I',
  '4': 'E',
  '5': 'F',
  '9': 'J'},
 {'3': 'D',
  '0': 'A',
  '6': 'G',
  '1': 'B',
  '7': 'H',
  '2': 'C',
  '8': 'I',
  '4': 'E',
  '5': 'F',
  '9': 'J'},
 Substitution 2d: {0: [[0]], 1: [[1]], 2: [[2]], 3: [[3]], 4: [[4]], 5:
 [[5]], 6: [[6]], 7: [[7]], 8: [[8]], 9: [[9]], 10: [[10]], 11: [[11]], 12:
 [[12]], 13: [[13]], 14: [[14]], 15: [[15]], 16: [[16]], 17: [[17]], 18: [[18]],
 19: [[19]], 20: [[20]], 21: [[21]], 22: [[22]], 23: [[23]]})

Introduction to Python/SageMath

2023-06-27T16:57:00Z

On Wednesday June 28th, 2023, I give short a Introduction to Python/SageMath as an online course organized by Pierre-Guy Plamondon in Mathematical Summer in Paris (MSP23) on WorkAdventure. Below is the material that will be presented or suggested.

Exercises:

Install and open a Jupyter notebook and do the User Interface Tour in the help menu.

Programming with Python. Here is a list of Jupyter notebooks to learn programming in Python: ProgrammingExercises.zip or ProgrammingExercises.tar.xz

Reproduce the computations made by BuzzFeedNews in a github repository of your choice, for instance about the fentanyl and cocaine overdose deaths (2018) or about The Tennis Racket (2016).

Solve some problems from the Project Euler. Project Euler contains more than 500 exercises that have to be solved with a computer

Reproduce one or more images from the matplotlib library.

Download the book Mathematical Computation with Sage by Paul Zimmermann et al. about the SageMath open source software. Reproduce the computations made in a section of your choice in the book.

Visit https://ask.sagemath.org/questions/ and try to reproduce some of the best answers to questions of interest for you.

Choose a section of your choice in the SageMath very large Reference Manual and reproduce the computations made in it.

When working on the above, two principles applies:

Once you finished solving a notebook or a problem on Project Euler on your own you need to explain your solution to at least one other person (who has already solved the same notebook or problem).

Once you reproduced the computation made by BuzzFeedNews, matplotlib image or some computation, you need to present and explain it to at least one other person.

Supplementary material:

Experimenting with Dynamical systems in SageMath: DynamicalSystemExercices.zip

Some more notebooks and exercices from this course given by Vincent Delecroix at AIMS in Rwanda (2016).

Découpe laser du chapeau, tuile apériodique découverte récemment

2023-05-25T11:57:00Z

Le chapeau est une tuile apériodique découverte par David Smith, Joseph Samuel Myers, Craig S. Kaplan, et Chaim Goodman-Strauss le 20 mars 2023. Suite à un exposé donné le 26 mars au National Museum of Mathematics, la nouvelle s'est vite répandue. En effet, cette découverte a été mentionnée les jours suivants dans des blogues puis dans Le New York Times le 28 mars, Le Monde le 29 mars, puis The Guardian et QuantaMagazine le 4 avril. Un vidéo de 20 minutes, réalisé par Passe-Science et publié début le 3 mai, explique le résultat et son contexte.

Déjà des articles proposant des résultats plus approfondis sur la tuile par des experts du domaine sont parus sur arXiv en mai 2023. Ils interprêtent les pavages comme des coupes et projection de réseaux de dimension supérieure. Le deuxième propose même une partition de la fenêtre de l'espace interne, un peu comme pour les pavages de Jeandel-Rao, à la différence qu'ici la partition a des bords fractales ce qui est pour moi une grande surprise.

Comme je faisais une intervention dans l'école de mon garçon à Bègles le 3 mai et au Lycée Kastler de Talence le 4 mai, j'ai réalisé un projet de découpe laser sur la tuile apériodique afin de partager cette récente découverte.

La première question était de construire un pavage d'un rectangle assez grand avec la pièce apériodique. Pour ce faire, j'ai ajouté un nouveau module dans mon package optionel au logiciel SageMath.

Le module réalise une réduction à une instance du problème de la couverture universelle, qui peut être résolu dans SageMath en utilisant l'algorithme des liens dansants de Donald Knuth, les solveurs SAT ou les programmes d'optimisation linéaire (solveur MILP). Le code utilise le système de coordonnées défini dans le fichier validate/kitegrid.pdf qui se trouve dans le code source associé à l'article.

Voici un exemple de construction d'un pavage avec la tuile apériodique. Le calcul est fait dans le logiciel SageMath muni de la version de développement de mon package optionnel slabbe qui peut être installé avec la commande sage -pip install slabbe. Ici, j'utilise le solveur SAT Glucose, développé au LaBRI. On peut installer glucose dans SageMath avec la commande sage -i glucose.

sage: from slabbe.aperiodic_monotile import MonotileSolver
sage: s = MonotileSolver(16, 17)
sage: G = s.draw_one_solution(solver='glucose')
sage: G.save('solution_16x17.png')
sage: G

Dans la manière de résoudre la question ci-haut, le problème est représenté par un problème de couverture exacte qui consiste à recouvrir exactement les entiers de 1 à n avec des sous-ensembles choisis dans une liste de sous-ensembles déterminés. Ici, on représente l'espace à recouvrir de manière discrète en comptant 6 points du plan par hexagone (un point pour chaque kite contenu dans un hexagone). Rappelons que la pièce Chapeau qui nous intéresse est formée d'une union d'exactement 8 de ces kites.

sage: s.plot_domain()

Ensuite, on construit une matrice de 0 et de 1 avec autant de colonnes que de points ci-haut (16 * 17 * 2 * 6 = 3264) et autant de lignes qu'il y a de copies isométriques de la pièce intersectant le domaine. Pour chaque copie de la pièce, une ligne dans la matrice contient des 1 exactement dans les colonnes associées aux kites occupés par la pièce.

sage: s.the_dlx_solver()
Dancing links solver for 3264 columns and 7116 rows

Le calcul ci-haut qui a construit la matrice (sparse) indique qu'il y a 7116 copies isométriques de la pièce qui intersectent (complètement ou partiellement) le domaine. Quand on voudra dessiner une solution, on ignorera les pièces incomplètes.

On peut maintenant résoudre le problème.

sage: s = MonotileSolver(8,8)
sage: %time L = s.one_solution()   # l'algo des liens dansants de Knuth est utilisé par défaut
CPU times: user 798 ms, sys: 32.2 ms, total: 830 ms
Wall time: 1min 20s

Le contenu d'une solution est une liste de nombres indiquant les lignes de la matrice de 0/1 à considérer pour former une solution. C'est-à-dire que la sous-matrice restreinte aux lignes données comporte exactement un 1 dans chaque colonne:

sage: L
[81,
 85,
 125,
 128,
 ...
 1772,
 1783,
 1794,
 1815]

Ici, il se trouve que les solveurs SAT sont plus efficaces que l'algo des liens dansants pour trouver une solution:

sage: %time L = s.one_solution(solver='glucose')
CPU times: user 326 ms, sys: 16.1 ms, total: 342 ms
Wall time: 526 ms
sage: %time L = s.one_solution(solver='kissat')
CPU times: user 335 ms, sys: 3.64 ms, total: 339 ms
Wall time: 461 ms

En effet, Glucose se comporte plutôt bien pour résoudre des problèmes de pavages du plan lorsqu'il existe une solution. Mais lorsqu'il n'y a pas de solution, l'algo des liens dansants de Knuth est parfois mieux. Aussi, l'algo des liens dansants de Knuth est très efficace pour énumérer toutes les solutions.

Le solveur Kissat a été ajouté dans SageMath par moi-même comme package optionnel cette année suite à une discussion avec Laurent Simon au café du LaBRI. On peut installer le solveur kissat dans SageMath avec la commande sage -i kissat.

Ici on extrait le contour des pièces d'une solution (tel que chaque arête est dessinée une seule fois afin d'éviter que la découpeuse laser passe deux fois par chaque arête ce qui peut endommager ou brûler le bord des pièces en bois) et on crée un fichier pdf ou svg. Je choisis une taille de 16 double-hexagones horizontalement et 17 verticalement, car cela crée un fichier qui correspond à une taille de 1m x 60cm. C'est la taille de la découpeuse laser à notre disposition:

sage: s = MonotileSolver(16, 17)
sage: tikz = s.one_solution_tikz(solver='glucose')
sage: tikz.pdf('solution_16x17.pdf')
sage: tikz.svg('solution_16x17.svg')     # or

/Files/2023/solution_16x17.svg

Avec l'aide de David Renault, mon collègue du LaBRI qui enseigne à l'ENSEIRB et qui m'a déjà accompagné dans la réalisation de projets de découpe laser, nous avons découpé le fichier ci-haut le jeudi 27 avril au EirLab, l'atelier de fabrication numérique (FabLab) de l'ENSEIRB-MATMECA:

Comme toujours, il faut quelque peu modifier le fichier svg dans Inkscape avant de lancer la découpe laser. Voici le fichier modifié juste avant la découpe.

Maintenant, on peut s'amuser avec les pièces:

Avec mes garçons, nous avons trouvé une forme intéressante qui recouvre le plan périodiquement à l'exception d'un trou hexagonal. Il se trouve que la même forme peut-être créée de deux façons différentes: sur l'image ci-bas la forme à droite est la globalement la même, mais elle n'est pas obtenue de la même façon que celle en haut à gauche. Pourtant, toutes deux ont le même contour extérieur et le même trou hexagonal.

Cette observation, déjà faite par d'autres, a mené au recouvrement d'une sphère avec la pièce et un trou pentagonal:

Factor complexity of words generated by multidimensional continued fraction algorithms

2022-11-03T11:11:00Z

I was asked by email how to compute with SageMath the factor complexity of words generated by multidimensional continued fraction algorithms. I'm copying my answer here so that I can more easily share it.

A) How to calculate the factor complexity of a word

To compute the complexity in factors, we need a finite word and not an infinite infinite word. In the example below, I take a prefix of the Fibonacci word and I compute the number of factors of size 100 and of size 0 to 19:

sage: w = words.FibonacciWord()
sage: w
word: 0100101001001010010100100101001001010010...
sage: prefix = w[:100000]
sage: prefix.number_of_factors(100)
101
sage: [prefix.number_of_factors(i) for i in range(20)]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]

The documentation for the number_of_factors method contains more examples, etc.

B) How to construct an S-adic word in SageMath

The method words.s_adic in SageMath allows to construct an S-adic sequence from a directive sequence, a set of substitutions and a sequence of first letters.

For example, we may use Kolakoski word as a directive sequence:

sage: directive_sequence = words.KolakoskiWord()
sage: directive_sequence
word: 1221121221221121122121121221121121221221...

Then, I define the Thue-Morse and Fibonacci substitutions:

sage: tm = WordMorphism('a->ab,b->ba')
sage: fib = WordMorphism('a->ab,b->a')
sage: tm
WordMorphism: a->ab, b->ba
sage: fib
WordMorphism: a->ab, b->a

Then, to define an S-adic sequence, I also need to define the sequence of first letters. Here, it is always the constant sequence a,a,a,a,...:

sage: from itertools import repeat
sage: letters = repeat('a')

I associate the letter 1 in the Kolakoski sequence to the Thue-Morse morphism and 2 to the Fibonacci morphism, this allows to construct an S-adic sequence:

sage: w = words.s_adic(directive_sequence, letters, {1:tm, 2:fib})
sage: w
word: abbaababbaabbaabbaababbaabbaababbaababba...

Then, as above, I can take a prefix and compute its factor complexity:

sage: prefix = w[:100000]
sage: [prefix.number_of_factors(i) for i in range(20)]
[1, 2, 4, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 34, 38]

C) Creating an S-adic sequence from Brun algorithm

With the package slabbe, you can construct an S-adic sequence from some of the known Multidimensional Continued Fraction Algorithm.

One can install it by running sage -pip install slabbe in a terminal where sage command exists. Sometimes this does not work.

Then, one may do:

sage: from slabbe.mult_cont_frac import Brun
sage: algo = Brun()
sage: algo
Brun 3-dimensional continued fraction algorithm
sage: D = algo.substitutions()
sage: D
{312: WordMorphism: 1->12, 2->2, 3->3,
 321: WordMorphism: 1->1, 2->21, 3->3,
 213: WordMorphism: 1->13, 2->2, 3->3,
 231: WordMorphism: 1->1, 2->2, 3->31,
 123: WordMorphism: 1->1, 2->23, 3->3,
 132: WordMorphism: 1->1, 2->2, 3->32}

sage: directive_sequence = algo.coding_iterator((1,e,pi))
sage: [next(directive_sequence) for _ in range(10)]
[123, 312, 312, 321, 132, 123, 312, 231, 231, 213]

Construction of the s-adic word from the substitutions and the directive sequence:

sage: from itertools import repeat
sage: D = algo.substitutions()
sage: directive_sequence = algo.coding_iterator((1,e,pi))
sage: words.s_adic(directive_sequence, repeat(1), D)
word: 1232323123233231232332312323123232312323...

Shortcut:

sage: algo.s_adic_word((1,e,pi))
word: 1232323123233231232332312323123232312323...

There are some more examples in the documentation.

This code was used in the creation of the 3-dimensional Continued Fraction Algorithms Cheat Sheets 7 years ago during my postdoc at Université de Liège, Belgium.

Using Glucose SAT solver to find a tiling of a rectangle by polyominoes

2022-06-20T09:41:00Z

In his Dancing links article, Donald Knuth considered the problem of packing 45 Y pentaminoes into a 15 x 15 square. We can redo this computation in SageMath using some implementation of his dancing links algorithm.

Dancing links takes 1.24 seconds to find a solution:

sage: from sage.combinat.tiling import Polyomino, TilingSolver
sage: y = Polyomino([(0,0),(1,0),(2,0),(3,0),(2,1)])
sage: T = TilingSolver([y], box=(15, 15), reusable=True, reflection=True)
sage: %time solution = next(T.solve())
CPU times: user 1.23 s, sys: 11.9 ms, total: 1.24 s
Wall time: 1.24 s

The first solution found is:

sage: sum(T.row_to_polyomino(row_number).show2d() for row_number in solution)

What is nice about dancing links algorithm is that it can list all solutions to a problem. For example, it takes less than 3 minutes to find all solutions of tiling a 15 x 15 rectangle with the Y polyomino:

sage: %time T.number_of_solutions()
CPU times: user 2min 46s, sys: 3.46 ms, total: 2min 46s
Wall time: 2min 46s
1696

It takes more time (38s) to find a first solution of a larger 20 x 20 rectangle:

sage: T = TilingSolver([y], box=(20,20), reusable=True, reflection=True)
sage: %time solution = next(T.solve())
CPU times: user 38.2 s, sys: 7.88 ms, total: 38.2 s
Wall time: 38.2 s

The polyomino tiling problem is reduced to an instance of the universal cover problem which is represented by a sparse matrix of 0 and 1:

sage: dlx = T.dlx_solver()
sage: dlx
Dancing links solver for 400 columns and 2584 rows

We observe that finding a solution to this problem takes the same amount of time. This is normal since it is exactly what is used behind the scene when calling next(T.solve()) above:

sage: %time sol = dlx.one_solution(ncpus=1)
CPU times: user 38.6 s, sys: 48 ms, total: 38.6 s
Wall time: 38.5 s

One way to improve the time it takes it to split the problem into parts and use many processors to work on each subproblems. Here a random column is used to split the problem which may affect the time it takes. Sometimes a good column is chosen and it works great as below, but sometimes it does not:

sage: %time sol = dlx.one_solution(ncpus=2)
CPU times: user 941 µs, sys: 32 ms, total: 32.9 ms
Wall time: 1.41 s

The reduction from dancing links instance to SAT instance #29338 and to MILP instance #29955 was merged into SageMath 9.2 during the last year. A discussion with Franco Saliola motivated me to implement these translations since he was also searching for faster way to solve dancing links problems. Indeed some problems are solved faster with other kind of solver, so it is good to make some comparisons between solvers.

Therefore, with a recent enough version of SageMath, we can now try to find a tiling with other kinds of solvers. Following my experience with tilings by Wang tiles, I know that Glucose SAT solver is quite efficient to solve tilings of the plane. This is why I test this one below. Glucose is now an optional package to SageMath which can be installed with:

sage -i glucose

Update (June 20th, 2022): It seems sage -i glucose no longer works. The new procedure is to use ./configure --enable-glucose when installation is made from source. See the question Unable to install glucose SAT solver with Sage on ask.sagemath.org for more information.

Glucose finds the solution of a 20 x 20 rectangle in 1.5 seconds:

sage: %time sol = dlx.one_solution_using_sat_solver('glucose')
CPU times: user 306 ms, sys: 12.1 ms, total: 319 ms
Wall time: 1.51 s

The rows of the solution found by Glucose are:

sage: sol
[0, 15, 19, 38, 74, 245, 270, 310, 320, 327, 332, 366, 419, 557, 582, 613, 660,
 665, 686, 699, 707, 760, 772, 774, 781, 802, 814, 816, 847, 855, 876, 905,
 1025, 1070, 1081, 1092, 1148, 1165, 1249, 1273, 1283, 1299, 1354, 1516, 1549,
 1599, 1609, 1627, 1633, 1650, 1717, 1728, 1739, 1773, 1795, 1891, 1908, 1918,
 1995, 2004, 2016, 2029, 2037, 2090, 2102, 2104, 2111, 2132, 2144, 2146, 2185,
 2235, 2301, 2460, 2472, 2498, 2538, 2548, 2573, 2583]

Each row correspond to a Y polyomino embedded in the plane in a certain position:

sage: sum(T.row_to_polyomino(row_number).show2d() for row_number in sol)

Glucose-Syrup (a parallelized version of Glucose) takes about the same time (1 second) to find a tiling of a 20 x 20 rectangle:

sage: T = TilingSolver([y], box=(20, 20), reusable=True, reflection=True)
sage: dlx = T.dlx_solver()
sage: dlx
Dancing links solver for 400 columns and 2584 rows
sage: %time sol = dlx.one_solution_using_sat_solver('glucose-syrup')
CPU times: user 285 ms, sys: 20 ms, total: 305 ms
Wall time: 1.09 s

Searching for a tiling of a 30 x 30 rectangle, Glucose takes 40s and Glucose-Syrup takes 16s while dancing links algorithm takes much longer (next(T.solve()) which is using dancing links algorithm does not halt in less than 5 minutes):

sage: T = TilingSolver([y], box=(30,30), reusable=True, reflection=True)
sage: dlx = T.dlx_solver()
sage: dlx
Dancing links solver for 900 columns and 6264 rows
sage: %time sol = dlx.one_solution_using_sat_solver('glucose')
CPU times: user 708 ms, sys: 36 ms, total: 744 ms
Wall time: 40.5 s
sage: %time sol = dlx.one_solution_using_sat_solver('glucose-syrup')
CPU times: user 754 ms, sys: 39.1 ms, total: 793 ms
Wall time: 16.1 s

Searching for a tiling of a 35 x 35 rectangle, Glucose takes 2min 5s and Glucose-Syrup takes 1min 16s:

sage: T = TilingSolver([y], box=(35, 35), reusable=True, reflection=True)
sage: dlx = T.dlx_solver()
sage: dlx
Dancing links solver for 1225 columns and 8704 rows
sage: %time sol = dlx.one_solution_using_sat_solver('glucose')
CPU times: user 1.07 s, sys: 47.9 ms, total: 1.12 s
Wall time: 2min 5s
sage: %time sol = dlx.one_solution_using_sat_solver('glucose-syrup')
CPU times: user 1.06 s, sys: 24 ms, total: 1.09 s
Wall time: 1min 16s

Here are the info of the computer used for the above timings (a 4 years old laptop runing Ubuntu 20.04):

$ lscpu
Architecture :                          x86_64
Mode(s) opératoire(s) des processeurs : 32-bit, 64-bit
Boutisme :                              Little Endian
Address size :                          39 bits physical, 48 bits virtual
Processeur(s) :                         8
Liste de processeur(s) en ligne :       0-7
Thread(s) par coeur :                   2
Coeur(s) par socket :                   4
Socket(s) :                             1
Noeud(s) NUMA :                         1
Identifiant constructeur :              GenuineIntel
Famille de processeur :                 6
Modèle :                                158
Nom de modèle :                         Intel(R) Core(TM) i7-7820HQ CPU @ 2.90GHz
Révision :                              9
Vitesse du processeur en MHz :          3549.025
Vitesse maximale du processeur en MHz : 3900,0000
Vitesse minimale du processeur en MHz : 800,0000
BogoMIPS :                              5799.77
Virtualisation :                        VT-x
Cache L1d :                             128 KiB
Cache L1i :                             128 KiB
Cache L2 :                              1 MiB
Cache L3 :                              8 MiB
Noeud NUMA 0 de processeur(s) :         0-7

To finish, I should mention that the implementation of dancing links made in SageMath is not the best one. Indeed, according to what Franco Saliola told me, the dancing links code written by Donald Knuth himself and available on his website (franco added some makefile to compile it more easily) is faster. It would be interesting to confirm this and if possible improves the implementation made in SageMath.

Installation de Python, Jupyter et JupyterLab

2021-02-23T11:15:00Z

L'École doctorale de mathématiques et informatique (EDMI) de l'Université de Bordeaux offre des cours chaque année. Dans ce cadre, cette année, je donnerai le cours Calcul et programmation avec Python ou SageMath et meilleures pratiques qui aura lieu les 25 février, 4 mars, 11 mars, 18 mars 2021 de 9h à 12h.

Le créneau du jeudi matin correspond au créneau des Jeudis Sage au LaBRI où un groupe d'utilisateurs de Python se rencontrent toutes les semaines pour faire du développement tout en posant des questions aux autres utilisateurs présents.

Le cours aura lieu sur le logiciel BigBlueButton auquel les participantEs inscritEs se connecteront par leur navigateur web (Mozilla Firefox ou Google Chrome). Selon les exigences minimales du client BigBlueButton, il faut éviter Safari ou IE, sinon certaines fonctionnalités ne marchent pas. Vous pouvez vous familiariser avec l'interface BigBlueButton en écoutant ce tutoriel BigBlueButton (sur youtube, 5 minutes). Consultez les pages de support suivantes en cas de soucis audio ou internet.

Pour la première séance, nous présenterons les bases de Python et les différentes interfaces. Nous ne pourrons pas passer trop de temps à faire l'installation des différents logiciels. Il serait donc préférable si les installations ont déjà été faites avant le cours par chacun des participantEs. Cela vous permettra de reproduire les commandes montrées et faire des exercices.

Les logiciels à installer avant le cours sont:

Python3

SageMath (facultatif)

IPython

Jupyter notebook classique

JupyterLab

Python 3: Normalement, Python est déjà installé sur votre ordinateur. Vous pouvez le confirmer en tapant python ou python3 dans un terminal (Linux/Mac) ou dans l'invité de commande (Windows). Vous devriez obtenir quelque chose qui ressemble à ceci:

Python 3.8.5 (default, Jul 28 2020, 12:59:40)
[GCC 9.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>

SageMath (facultatif): SageMath est un logiciel libre de mathématiques basé sur Python et regroupant des centaines de packages et librairies. Il y a plusieurs manières d'installer SageMath, et je vous recommande de lire cette documentation pour déterminer la manière de l'installer qui vous convient le mieux. Sinon, vous pouvez télécharger directement les binaires ici.

Vous devriez obtenir quelque chose qui ressemble à ceci:

┌────────────────────────────────────────────────────────────────────┐
│ SageMath version 9.2, Release Date: 2020-10-24                     │
│ Using Python 3.8.5. Type "help()" for help.                        │
└────────────────────────────────────────────────────────────────────┘
sage:

IPython:

Si vous avez déjà installé SageMath, c'est bon, car ipython en fait partie. La commande sage -ipython vous permettra de l'ouvrir.

Si vous n'avez pas SageMath, vous pouvez l'installer via pip install ipython ou sinon en suivant ces instructions du site ipython. Ensuite, la commande ipython dans le terminal (Linux, OS X) ou dans l'invité de commande (Windows) vous permettra de l'ouvrir.

Vous devriez obtenir quelque chose qui ressemble à ceci:

Python 3.8.5 (default, Jul 28 2020, 12:59:40)
Type 'copyright', 'credits' or 'license' for more information
IPython 7.13.0 -- An enhanced Interactive Python. Type '?' for help.

In [1]:

Jupyter:

Si vous avez déjà installé SageMath, c'est bon, car Jupyter en fait partie. La commande sage -n jupyter vous permettra de l'ouvrir.

Si vous n'avez pas SageMath, vous pouvez suivre ces instructions du site jupyter.org. Ensuite, la commande jupyter notebook dans le terminal (Linux, OS X) ou dans l'invité de commande (Windows) vous permettra de l'ouvrir.

Vous devriez obtenir quelque chose qui ressemble à ceci dans votre navigateur:

JupyterLab:

Si vous avez déjà installé SageMath, vous pouvez installer JupyterLab en faisant sage -i jupyterlab et l'ouvrir en faisant sage -n jupyterlab. Sur Windows, c'est un tout petit peut différent, il faut plutôt faire pip install jupyterlab dans la console SageMath selon cette récente réponse sur ask.sagemath.org.

Si vous n'avez pas SageMath, vous pouvez suivre les instructions du même site que ci-haut. Ensuite, la commande jupyter-lab ou jupyter lab dans le terminal (Linux, OS X) ou dans l'invité de commande (Windows) vous permettra de l'ouvrir.

Vous devriez obtenir quelque chose qui ressemble à ceci dans votre navigateur:

Tiling a polyomino with polyominoes in SageMath

2020-12-03T13:48:00Z

Suppose that you 3D print many copies of the following 3D hexo-mino at home:

sage: from sage.combinat.tiling import Polyomino, TilingSolver
sage: p = Polyomino([(0,0,0), (0,1,0), (1,0,0), (2,0,0), (2,1,0), (2,1,1)], color='blue')
sage: p.show3d()
Launched html viewer for Graphics3d Object

You would like to know if you can tile a larger polyomino or in particular a rectangular box with many copies of it. The TilingSolver module in SageMath is made for that. See also this recent question on ask.sagemath.org.

sage: T = TilingSolver([p], (7,5,3), rotation=True, reflection=False, reusable=True)
sage: T
Tiling solver of 1 pieces into a box of size 24
Rotation allowed: True
Reflection allowed: False
Reusing pieces allowed: True

There is no solution when tiling a box of shape 7x5x3 with this polyomino:

sage: T.number_of_solutions()
0

But there are 4 solutions when tiling a box of shape 4x3x2 with this polyomino:

sage: T = TilingSolver([p], (4,3,2), rotation=True, reflection=False, reusable=True)
sage: T.number_of_solutions()
4

We construct the list of solutions:

sage: solutions = [sol for sol in T.solve()]

Each solution contains the isometric copies of the polyominoes tiling the box:

sage: solutions[0]
[Polyomino: [(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 1, 0), (2, 0, 0), (2, 1, 0)], Color: #ff0000,
 Polyomino: [(0, 1, 1), (0, 2, 0), (0, 2, 1), (1, 1, 1), (2, 1, 1), (2, 2, 1)], Color: #ff0000,
 Polyomino: [(1, 0, 0), (1, 0, 1), (2, 0, 1), (3, 0, 0), (3, 0, 1), (3, 1, 0)], Color: #ff0000,
 Polyomino: [(1, 2, 0), (1, 2, 1), (2, 2, 0), (3, 1, 1), (3, 2, 0), (3, 2, 1)], Color: #ff0000]

It may be easier to visualize the solutions, so we define the following function allowing to draw the solutions with different colors for each piece:

sage: def draw_solution(solution, size=0.9):
....:     colors = rainbow(len(solution))
....:     for piece,col in zip(solution, colors):
....:         piece.color(col)
....:     return sum((piece.show3d(size=size) for piece in solution), Graphics())

sage: G = [draw_solution(sol) for sol in solutions]
sage: G
[Graphics3d Object, Graphics3d Object, Graphics3d Object, Graphics3d Object]

sage: G[0]   # in Sage, this will open a 3d viewer automatically

sage: G[1]

sage: G[2]

sage: G[3]

We may save the solutions to a file:

sage: G[0].save('solution0.png', aspect_ratio=1, zoom=1.2)
sage: G[1].save('solution1.png', aspect_ratio=1, zoom=1.2)
sage: G[2].save('solution2.png', aspect_ratio=1, zoom=1.2)
sage: G[3].save('solution3.png', aspect_ratio=1, zoom=1.2)

Question: are all of the 4 solutions isometric to each other?

The tiling problem is solved due to a reduction to the exact cover problem for which dancing links Knuth's algorithm provides all the solutions. One can see the rows of the dancing links matrix as follows:

sage: d = T.dlx_solver()
sage: d
Dancing links solver for 24 columns and 56 rows
sage: d.rows()
[[0, 1, 2, 4, 5, 11],
 [6, 7, 8, 10, 11, 17],
 [12, 13, 14, 16, 17, 23],
 ...
 [4, 6, 7, 9, 10, 11],
 [10, 12, 13, 15, 16, 17],
 [16, 18, 19, 21, 22, 23]]

The solutions to the dlx solver can be obtained as follows:

sage: it = d.solutions_iterator()
sage: next(it)
[3, 36, 19, 52]

These are the indices of the rows each corresponding to an isometric copy of the polyomino within the box.

Since SageMath-9.2, the possibility to reduce the problem to a MILP problem or a SAT instance was added to SageMath (see #29338 and #29955):

sage: d.to_milp()
(Boolean Program (no objective, 56 variables, 24 constraints),
 MIPVariable of dimension 1)
sage: d.to_sat_solver()
CryptoMiniSat solver: 56 variables, 2348 clauses.

Computer experiments for the Lyapunov exponent for MCF algorithms when dimension is larger than 3

2020-03-27T13:00:00Z

In November 2015, I wanted to share intuitions I developped on the behavior of various distinct Multidimensional Continued Fractions algorithms obtained from various kind of experiments performed with them often involving combinatorics and digitial geometry but also including the computation of their first two Lyapunov exponents.

As continued fractions are deeply related to the combinatorics of Sturmian sequences which can be seen as the digitalization of a straight line in the grid \(\mathbb{Z}^2\), the multidimensional continued fractions algorithm are related to the digitalization of a straight line and hyperplanes in \(\mathbb{Z}^d\).

This is why I shared those experiments in what I called 3-dimensional Continued Fraction Algorithms Cheat Sheets because of its format inspired from typical cheat sheets found on the web. All of the experiments can be reproduced using the optional SageMath package slabbe where I share my research code. People asked me whether I was going to try to publish those Cheat Sheets, but I was afraid the format would change the organization of the information and data in each page, so, in the end, I never submitted those Cheat Sheets anywhere.

Here I should say that \(d\) stands for the dimension of the vector space on which the involved matrices act and \(d-1\) is the dimension of the projective space on which the algorithm acts.

One of the consequence of the Cheat Sheets is that it made us realize that the algorithm proposed by Julien Cassaigne had the same first two Lyapunov exponents as the Selmer algorithm (first 3 significant digits were the same). Julien then discovered the explanation as its algorithm is conjugated to some semi-sorted version of the Selmer algorihm. This result was shared during WORDS 2017 conference. Julien Leroy, Julien Cassaigne and I are still working on the extended version of the paper. It is taking longer mainly because of my fault because I have been working hard on aperiodic Wang tilings in the previous 2 years.

During July 2019, Wolfgang, Valérie and Jörg asked me to perform computations of the first two Lyapunov exponents for \(d\)-dimensional Multidimensional Continued Fraction algorithms for \(d\) larger than 3. The main question of interest is whether the second Lyapunov exponent keeps being negative as the dimension increases. This property is related to the notion of strong convergence almost everywhere of the simultaneous diopantine approximations provided by the algorithm of a fixed vector of real numbers. It did not take me too long to update my package since I had started to generalize my code to larger dimensions during Fall 2017. It turns out that, as the dimension increases, all known MCF algorithms have their second Lyapunov exponent become positive. My computations were thus confirming what they eventually published in their preprint in November 2019.

My motivation for sharing the results is the conference Multidimensional Continued Fractions and Euclidean Dynamics held this week (supposed to be held in Lorentz Center, March 23-27 2020, it got cancelled because of the corona virus) where some discussions during video meetings are related to this subject.

The computations performed below can be summarized in one graphics showing the values of \(1-\theta_2/\theta_1\) with respect to \(d\) for various \(d\)-dimensional MCF algorithms. It seems that \(\theta_2\) is negative up to dimension 10 for Brun, up to dimension 4 for Selmer and up to dimension 5 for ARP.

I have to say that I was disapointed by the results because the algorithm Arnoux-Rauzy-Poincaré (ARP) that Valérie and I introduced was not performing so well as its second Lyapunov exponent seems to become positive for dimension \(d\geq 6\). I had good expectations for ARP because it reaches the highest value for \(1-\theta_2/\theta_1\) in the computations performed in the Cheat Sheets, thus better than Brun, better than Selmer when \(d=3\).

The algorithm for the computation of the first two Lyapunov exponents was provided to me by Vincent Delecroix. It applies the algorithm \((v,w)\mapsto(M^{-1}v,M^T w)\) millions of times. The evolution of the size of the vector \(v\) gives the first Lyapunov exponent. The evolution of the size of the vector \(w\) gives the second Lyapunov exponent. Since the computation is performed on 64-bits double floating point number, their are numerical issues to deal with. This is why some Gramm Shimdts operation is performed on the vector \(w\) at each time the vectors are renormalized to keep the vector \(w\) orthogonal to \(v\). Otherwise, the numerical errors cumulate and the computed value for the \(\theta_2\) becomes the same as \(\theta_1\). You can look at the algorithm online starting at line 1723 of the file mult_cont_frac_pyx.pyx from my optional package.

I do not know from where Vincent took that algorithm. So, I do not know how exact it is and whether there exits any proof of lower bounds and upper bounds on the computations being performed. What I can say is that it is quite reliable in the sense that is returns the same values over and over again (by that I mean 3 common most significant digits) with any fixed inputs (number of iterations).

Below, I show the code illustrating how to reproduce the results.

The version 0.6 (November 2019) of my package slabbe includes the necessary code to deal with some \(d\)-dimensional Multidimensional Continued Fraction (MCF) algorithms. Its documentation is available online. It is a PIP package, so it can be installed like this:

sage -pip install slabbe

Recall that the dimension \(d\) below is the linear one and \(d-1\) is the dimension of the space for the corresponding projective algorithm.

Import the Brun, Selmer and Arnoux-Rauzy-Poincaré MCF algorithms from the optional package:

sage: from slabbe.mult_cont_frac import Brun, Selmer, ARP

The computation of the first two Lyapunov exponents performed on one single orbit:

sage: Brun(dim=3).lyapunov_exponents(n_iterations=10^7)
(0.30473782969922547, -0.11220958022368056, 1.3682167728713919)

The starting point is taken randomly, but the results of the form of a 3-tuple \((\theta_1,\theta_2,1-\theta_2/\theta_1)\) are about the same:

sage: Brun(dim=3).lyapunov_exponents(n_iterations=10^7)
(0.30345018206132324, -0.11171509867725296, 1.3681497170915415)

Increasing the dimension \(d\) yields:

sage: Brun(dim=4).lyapunov_exponents(n_iterations=10^7)
(0.32639514522732005, -0.07191456560115839, 1.2203297648654456)
sage: Brun(dim=5).lyapunov_exponents(n_iterations=10^7)
(0.30918877340506756, -0.0463930802132972, 1.1500477514185734)

It performs an orbit of length \(10^7\) in about .5 seconds, of length \(10^8\) in about 5 seconds and of length \(10^9\) in about 50 seconds:

sage: %time Brun(dim=3).lyapunov_exponents(n_iterations=10^7)
CPU times: user 540 ms, sys: 0 ns, total: 540 ms
Wall time: 539 ms
(0.30488799356325225, -0.11234354880132114, 1.3684748208296182)
sage: %time Brun(dim=3).lyapunov_exponents(n_iterations=10^8)
CPU times: user 5.09 s, sys: 0 ns, total: 5.09 s
Wall time: 5.08 s
(0.30455473631148755, -0.11217550411862384, 1.3683262505689446)
sage: %time Brun(dim=3).lyapunov_exponents(n_iterations=10^9)
CPU times: user 51.2 s, sys: 0 ns, total: 51.2 s
Wall time: 51.2 s
(0.30438755982577026, -0.11211562816821799, 1.368331834035505)

Here, in what follows, I must admit that I needed to do a small fix to my package, so the code below will not work in version 0.6 of my package, I will update my package in the next days in order that the computations below can be reproduced:

sage: from slabbe.lyapunov import lyapunov_comparison_table

For each \(3\leq d\leq 20\), I compute 30 orbits and I show the most significant digits and the standard deviation of the 30 values computed.

For Brun algorithm:

sage: algos = [Brun(d) for d in range(3,21)]
sage: %time lyapunov_comparison_table(algos, n_orbits=30, n_iterations=10^7, ncpus=8)
CPU times: user 190 ms, sys: 2.8 s, total: 2.99 s
Wall time: 6min 31s
  Algorithm     \#Orbits   $\theta_1$ (std)     $\theta_2$ (std)      $1-\theta_2/\theta_1$ (std)
+-------------+----------+--------------------+---------------------+-----------------------------+
  Brun (d=3)    30         0.3045 (0.00040)     -0.1122 (0.00017)     1.3683 (0.00022)
  Brun (d=4)    30         0.32632 (0.000055)   -0.07188 (0.000051)   1.2203 (0.00014)
  Brun (d=5)    30         0.30919 (0.000032)   -0.04647 (0.000041)   1.1503 (0.00013)
  Brun (d=6)    30         0.28626 (0.000027)   -0.03043 (0.000035)   1.1063 (0.00012)
  Brun (d=7)    30         0.26441 (0.000024)   -0.01966 (0.000027)   1.0743 (0.00010)
  Brun (d=8)    30         0.24504 (0.000027)   -0.01207 (0.000024)   1.04926 (0.000096)
  Brun (d=9)    30         0.22824 (0.000021)   -0.00649 (0.000026)   1.0284 (0.00012)
  Brun (d=10)   30         0.2138 (0.00098)     -0.0022 (0.00015)     1.0104 (0.00074)
  Brun (d=11)   30         0.20085 (0.000015)   0.00106 (0.000022)    0.9947 (0.00011)
  Brun (d=12)   30         0.18962 (0.000017)   0.00368 (0.000021)    0.9806 (0.00011)
  Brun (d=13)   30         0.17967 (0.000011)   0.00580 (0.000020)    0.9677 (0.00011)
  Brun (d=14)   30         0.17077 (0.000011)   0.00755 (0.000021)    0.9558 (0.00012)
  Brun (d=15)   30         0.16278 (0.000012)   0.00900 (0.000017)    0.9447 (0.00010)
  Brun (d=16)   30         0.15556 (0.000011)   0.01022 (0.000013)    0.93433 (0.000086)
  Brun (d=17)   30         0.149002 (9.5e-6)    0.01124 (0.000015)    0.9246 (0.00010)
  Brun (d=18)   30         0.14303 (0.000010)   0.01211 (0.000019)    0.9153 (0.00014)
  Brun (d=19)   30         0.13755 (0.000012)   0.01285 (0.000018)    0.9065 (0.00013)
  Brun (d=20)   30         0.13251 (0.000011)   0.01349 (0.000019)    0.8982 (0.00014)

For Selmer algorithm:

sage: algos = [Selmer(d) for d in range(3,21)]
sage: %time lyapunov_comparison_table(algos, n_orbits=30, n_iterations=10^7, ncpus=8)
CPU times: user 203 ms, sys: 2.78 s, total: 2.98 s
Wall time: 6min 27s
  Algorithm       \#Orbits   $\theta_1$ (std)     $\theta_2$ (std)      $1-\theta_2/\theta_1$ (std)
+---------------+----------+--------------------+---------------------+-----------------------------+
  Selmer (d=3)    30         0.1827 (0.00041)     -0.0707 (0.00017)     1.3871 (0.00029)
  Selmer (d=4)    30         0.15808 (0.000058)   -0.02282 (0.000036)   1.1444 (0.00023)
  Selmer (d=5)    30         0.13199 (0.000033)   0.00176 (0.000034)    0.9866 (0.00026)
  Selmer (d=6)    30         0.11205 (0.000017)   0.01595 (0.000036)    0.8577 (0.00031)
  Selmer (d=7)    30         0.09697 (0.000012)   0.02481 (0.000030)    0.7442 (0.00032)
  Selmer (d=8)    30         0.085340 (8.5e-6)    0.03041 (0.000032)    0.6437 (0.00036)
  Selmer (d=9)    30         0.076136 (5.9e-6)    0.03379 (0.000032)    0.5561 (0.00041)
  Selmer (d=10)   30         0.068690 (5.5e-6)    0.03565 (0.000023)    0.4810 (0.00032)
  Selmer (d=11)   30         0.062557 (4.4e-6)    0.03646 (0.000021)    0.4172 (0.00031)
  Selmer (d=12)   30         0.057417 (3.6e-6)    0.03654 (0.000017)    0.3636 (0.00028)
  Selmer (d=13)   30         0.05305 (0.000011)   0.03615 (0.000018)    0.3186 (0.00032)
  Selmer (d=14)   30         0.04928 (0.000060)   0.03546 (0.000051)    0.2804 (0.00040)
  Selmer (d=15)   30         0.046040 (2.0e-6)    0.03462 (0.000013)    0.2482 (0.00027)
  Selmer (d=16)   30         0.04318 (0.000011)   0.03365 (0.000014)    0.2208 (0.00028)
  Selmer (d=17)   30         0.040658 (3.3e-6)    0.03263 (0.000013)    0.1974 (0.00030)
  Selmer (d=18)   30         0.038411 (2.7e-6)    0.031596 (9.8e-6)     0.1774 (0.00022)
  Selmer (d=19)   30         0.036399 (2.2e-6)    0.030571 (8.0e-6)     0.1601 (0.00019)
  Selmer (d=20)   30         0.0346 (0.00011)     0.02955 (0.000093)    0.1452 (0.00019)

For Arnoux-Rauzy-Poincaré algorithm:

sage: algos = [ARP(d) for d in range(3,21)]
sage: %time lyapunov_comparison_table(algos, n_orbits=30, n_iterations=10^7, ncpus=8)
CPU times: user 226 ms, sys: 2.76 s, total: 2.99 s
Wall time: 13min 20s
  Algorithm                        \#Orbits   $\theta_1$ (std)     $\theta_2$ (std)      $1-\theta_2/\theta_1$ (std)
+--------------------------------+----------+--------------------+---------------------+-----------------------------+
  Arnoux-Rauzy-Poincar\'e (d=3)    30         0.4428 (0.00056)     -0.1722 (0.00025)     1.3888 (0.00016)
  Arnoux-Rauzy-Poincar\'e (d=4)    30         0.6811 (0.00020)     -0.16480 (0.000085)   1.24198 (0.000093)
  Arnoux-Rauzy-Poincar\'e (d=5)    30         0.7982 (0.00012)     -0.0776 (0.00010)     1.0972 (0.00013)
  Arnoux-Rauzy-Poincar\'e (d=6)    30         0.83563 (0.000091)   0.0475 (0.00010)      0.9432 (0.00012)
  Arnoux-Rauzy-Poincar\'e (d=7)    30         0.8363 (0.00011)     0.1802 (0.00016)      0.7845 (0.00020)
  Arnoux-Rauzy-Poincar\'e (d=8)    30         0.8213 (0.00013)     0.3074 (0.00023)      0.6257 (0.00028)
  Arnoux-Rauzy-Poincar\'e (d=9)    30         0.8030 (0.00012)     0.4205 (0.00017)      0.4763 (0.00022)
  Arnoux-Rauzy-Poincar\'e (d=10)   30         0.7899 (0.00011)     0.5160 (0.00016)      0.3467 (0.00020)
  Arnoux-Rauzy-Poincar\'e (d=11)   30         0.7856 (0.00014)     0.5924 (0.00020)      0.2459 (0.00022)
  Arnoux-Rauzy-Poincar\'e (d=12)   30         0.7883 (0.00010)     0.6497 (0.00012)      0.1759 (0.00014)
  Arnoux-Rauzy-Poincar\'e (d=13)   30         0.7930 (0.00010)     0.6892 (0.00014)      0.1309 (0.00014)
  Arnoux-Rauzy-Poincar\'e (d=14)   30         0.7962 (0.00012)     0.7147 (0.00015)      0.10239 (0.000077)
  Arnoux-Rauzy-Poincar\'e (d=15)   30         0.7974 (0.00012)     0.7309 (0.00014)      0.08340 (0.000074)
  Arnoux-Rauzy-Poincar\'e (d=16)   30         0.7969 (0.00015)     0.7411 (0.00014)      0.07010 (0.000048)
  Arnoux-Rauzy-Poincar\'e (d=17)   30         0.7960 (0.00014)     0.7482 (0.00014)      0.06005 (0.000050)
  Arnoux-Rauzy-Poincar\'e (d=18)   30         0.7952 (0.00013)     0.7537 (0.00014)      0.05218 (0.000046)
  Arnoux-Rauzy-Poincar\'e (d=19)   30         0.7949 (0.00012)     0.7584 (0.00013)      0.04582 (0.000035)
  Arnoux-Rauzy-Poincar\'e (d=20)   30         0.7948 (0.00014)     0.7626 (0.00013)      0.04058 (0.000025)

The computation of the figure shown above is done with the code below:

sage: brun_list = [1.3683, 1.2203, 1.1503, 1.1063, 1.0743, 1.04926, 1.0284, 1.0104, 0.9947, 0.9806, 0.9677, 0.9558, 0.9447, 0.93433, 0.9246, 0.9153, 0.9065, 0.8982]
sage: selmer_list = [ 1.3871, 1.1444, 0.9866, 0.8577, 0.7442, 0.6437, 0.5561, 0.4810, 0.4172, 0.3636, 0.3186, 0.2804, 0.2482, 0.2208, 0.1974, 0.1774, 0.1601, 0.1452]
sage: arp_list = [1.3888, 1.24198, 1.0972, 0.9432, 0.7845, 0.6257, 0.4763, 0.3467, 0.2459, 0.1759, 0.1309, 0.10239, 0.08340, 0.07010, 0.06005, 0.05218, 0.04582, 0.04058]
sage: brun_points = list(enumerate(brun_list, start=3))
sage: selmer_points = list(enumerate(selmer_list, start=3))
sage: arp_points = list(enumerate(arp_list, start=3))
sage: G = Graphics()
sage: G += plot(1+1/(x-1), x, 3, 20, legend_label='Optimal algo:$1+1/(d-1)$', linestyle='dashed', color='blue', thickness=3)
sage: G += line([(3,1), (20,1)], color='black', legend_label='Strong convergence threshold', linestyle='dotted', thickness=2)
sage: G += line(brun_points, legend_label='Brun', color='cyan', thickness=3)
sage: G += line(selmer_points, legend_label='Selmer', color='green', thickness=3)
sage: G += line(arp_points, legend_label='ARP', color='red', thickness=3)
sage: G.ymin(0)
sage: G.axes_labels(['$d$',''])
sage: G.show(title='Computation of first 2 Lyapunov Exponents: comparison of the value $1-\\theta_2/\\theta_1$\n for $d$-dimensional MCF algorithms Brun, Selmer and ARP for $3\\leq d\\leq 20$')

Comment installer et utiliser RISE, une extension du notebook Jupyter pour faire des présentations

2019-01-24T10:37:00Z

La semaine dernière, Jeroen Demeyer a fait une présentation lors de l'Atelier PARI/GP 2019 au sujet de cypari2.

La présentation de Jeroen consistait en des diapositives HTML où les calculs sont faits en direct (avec Jupyter) et où on peut les modifier en direct dans les diapositives. Impressionant! Tout cela grâce au package Python RISE.

Pour installer et utiliser RISE, une extension du Jupyter Notebook pour faire des présentations éditables, il ne suffit pas de l'installer il faut aussi recopier les css au bon endroit. Pour l'installer dans Sage, il suffit de faire:

sage -pip install rise
sage -sh
jupyter-nbextension install rise --py --sys-prefix

Après on peut consulter ce démo sur youtube et la documentation de RISE est ici.

Comparison of Wang tiling solvers

2018-12-12T15:24:00Z

During the last year, I have written a Python module to deal with Wang tiles containing about 4K lines of code including doctests and documentation.

It can be installed like this:

sage -pip install slabbe

It can be used like this:

sage: from slabbe import WangTileSet
sage: tiles = [(2,4,2,1), (2,2,2,0), (1,1,3,1), (1,2,3,2), (3,1,3,3),
....: (0,1,3,1), (0,0,0,1), (3,1,0,2), (0,2,1,2), (1,2,1,4), (3,3,1,2)]
sage: T0 = WangTileSet([tuple(str(a) for a in t) for t in tiles])
sage: T0.tikz(ncolumns=11).pdf()

/Files/2018/T0_tiles.svg

The module on wang tiles contains a class WangTileSolver which contains three reductions of the Wang tiling problem the first using MILP solvers, the second using SAT solvers and the third using Knuth's dancing links.

Here is one example of a tiling found using the dancing links reduction:

sage: %time tiling = T0.solver(10,10).solve(solver='dancing_links')
CPU times: user 36 ms, sys: 12 ms, total: 48 ms
Wall time: 65.5 ms
sage: tiling.tikz().pdf()

/Files/2018/T0_10x10tiling.svg

All these reductions now allow me to compare the efficiency of various types of solvers restricted to the Wang tiling type of problems. Here is the list of solvers that I often use.

List of solvers
Solver	Description
`'Gurobi'`	MILP solver
`'GLPK'`	MILP solver
`'PPL'`	MILP solver
`'LP'`	a SAT solver using a reduction to LP
`'cryptominisat'`	SAT solver
`'picosat'`	SAT solver
`'glucose'`	SAT solver
`'dancing_links'`	Knuth's algorihm

In this recent work on the substitutive structure of Jeandel-Rao tilings, I introduced various Wang tile sets \(T_i\) for \(i\in\{0,1,\dots,12\}\). In this blog post, we will concentrate on the 11 Wang tile set \(T_0\) introduced by Jeandel and Rao as well as \(T_2\) containing 20 tiles and \(T_3\) containing 24 tiles.

Tiling a n x n square

The most natural question to ask is to find valid Wang tilings of \(n\times n\) square with given Wang tiles. Below is the time spent by each mentionned solvers to find a valid tiling of a \(n\times n\) square in less than 10 seconds for each of the three wang tile sets \(T_0\), \(T_2\) and \(T_3\).

/Files/2018/T0_square_tilings.svg /Files/2018/T2_square_tilings.svg /Files/2018/T3_square_tilings.svg

We remark that MILP solvers are slower. Dancing links can solve 20x20 squares with Jeandel Rao tiles \(T_0\) and SAT solvers are performing very well with Glucose being the best as it can find a 55x55 tiling with Jeandel-Rao tiles \(T_0\) in less than 10 seconds.

Finding all dominoes allowing a surrounding of given radius

One thing that is often needed in my research is to enumerate all horizontal and vertical dominoes that allow a given surrounding radius. This is a difficult question in general as deciding if a given tile set admits a tiling of the infinite plane is undecidable. But in some cases, the information we get from the dominoes admitting a surrounding of radius 1, 2, 3 or 4 is enough to conclude that the tiling can be desubstituted for instance. This is why we need to answer this question as fast as possible.

Below is the comparison in the time taken by each solver to compute all vertical and horizontal dominoes allowing a surrounding of radius 1, 2 and 3 (in less than 1000 seconds for each execution).

/Files/2018/T0_dominoes_surrounding.svg /Files/2018/T2_dominoes_surrounding.svg /Files/2018/T3_dominoes_surrounding.svg

What is surprising at first is that the solvers that performed well in the first \(n\times n\) square experience are not the best in the second experiment computing valid dominoes. Dancing links and the MILP solver Gurobi are now the best algorithms to compute all dominoes. They are followed by picosat and cryptominisat and then glucose.

The source code of the above comparisons

The source code of the above comparison can be found in this Jupyter notebook. Note that it depends on the use of Glucose as a Sage optional package (#26361) and on the most recent development version of slabbe optional Sage Package.

Wooden laser-cut Jeandel-Rao tiles

2018-09-07T09:16:00Z

I have been working on Jeandel-Rao tiles lately.

/Files/2018/article2_T0_tiles.svg

Before the conference Model Sets and Aperiodic Order held in Durham UK (Sep 3-7 2018), I thought it would be a good idea to bring some real tiles at the conference. So I first decided of some conventions to represent the above tiles as topologically closed disk basically using the representation of integers in base 1:

/Files/2018/T0_shapes.svg

With these shapes, I created a 33 x 19 patch. With 3cm on each side, the patch takes 99cm x 57cm just within the capacity of the laser cut machine (1m x 60 cm):

/Files/2018/33x19_A_scale3.svg

With the help of David Renault from LaBRI, we went at Coh@bit, the FabLab of Bordeaux University and we laser cut two 3mm thick plywood for a total of 1282 Wang tiles. This is the result:

One may recreate the 33 x 19 tiling as follows (note that I am using Cartesian-like coordinates, so the first list data[0] actually is the first column from bottom to top):

sage: data = [[10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 2, 6, 1, 3, 8, 7, 0, 9, 7],
....:  [4, 5, 6, 1, 8, 10, 4, 0, 9, 3, 8, 7, 0, 9, 7, 5, 0, 9, 3],
....:  [3, 7, 6, 1, 7, 2, 5, 0, 9, 8, 7, 5, 0, 9, 3, 7, 0, 9, 10],
....:  [10, 4, 6, 1, 3, 8, 7, 0, 9, 7, 5, 6, 1, 8, 10, 4, 0, 9, 3],
....:  [2, 5, 6, 1, 8, 7, 5, 0, 9, 3, 7, 6, 1, 7, 2, 5, 0, 9, 8],
....:  [8, 7, 6, 1, 7, 5, 6, 1, 8, 10, 4, 6, 1, 3, 8, 7, 0, 9, 7],
....:  [7, 5, 6, 1, 3, 7, 6, 1, 7, 2, 5, 6, 1, 8, 7, 5, 0, 9, 3],
....:  [3, 7, 6, 1, 10, 4, 6, 1, 3, 8, 7, 6, 1, 7, 5, 6, 1, 8, 10],
....:  [10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 5, 6, 1, 3, 7, 6, 1, 7, 2],
....:  [2, 5, 6, 1, 8, 10, 4, 0, 9, 3, 7, 6, 1, 10, 4, 6, 1, 3, 8],
....:  [8, 7, 6, 1, 7, 5, 5, 0, 9, 10, 4, 6, 1, 3, 3, 7, 0, 9, 7],
....:  [7, 5, 6, 1, 3, 7, 6, 1, 10, 4, 5, 6, 1, 8, 10, 4, 0, 9, 3],
....:  [3, 7, 6, 1, 10, 4, 6, 1, 3, 3, 7, 6, 1, 7, 2, 5, 0, 9, 8],
....:  [10, 4, 6, 1, 3, 3, 7, 0, 9, 10, 4, 6, 1, 3, 8, 7, 0, 9, 7],
....:  [4, 5, 6, 1, 8, 10, 4, 0, 9, 3, 3, 7, 0, 9, 7, 5, 0, 9, 3],
....:  [3, 7, 6, 1, 7, 2, 5, 0, 9, 8, 10, 4, 0, 9, 3, 7, 0, 9, 10],
....:  [10, 4, 6, 1, 3, 8, 7, 0, 9, 7, 5, 5, 0, 9, 10, 4, 0, 9, 3],
....:  [2, 5, 6, 1, 8, 7, 5, 0, 9, 3, 7, 6, 1, 10, 4, 5, 0, 9, 8],
....:  [8, 7, 6, 1, 7, 5, 6, 1, 8, 10, 4, 6, 1, 3, 3, 7, 0, 9, 7],
....:  [7, 5, 6, 1, 3, 7, 6, 1, 7, 2, 5, 6, 1, 8, 10, 4, 0, 9, 3],
....:  [3, 7, 6, 1, 10, 4, 6, 1, 3, 8, 7, 6, 1, 7, 2, 5, 0, 9, 8],
....:  [10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 2, 6, 1, 3, 8, 7, 0, 9, 7],
....:  [4, 5, 6, 1, 8, 10, 4, 0, 9, 3, 8, 7, 0, 9, 7, 5, 0, 9, 3],
....:  [3, 7, 6, 1, 7, 2, 5, 0, 9, 8, 7, 5, 0, 9, 3, 7, 0, 9, 10],
....:  [10, 4, 6, 1, 3, 8, 7, 0, 9, 7, 5, 6, 1, 8, 10, 4, 0, 9, 3],
....:  [3, 3, 7, 0, 9, 7, 5, 0, 9, 3, 7, 6, 1, 7, 2, 5, 0, 9, 8],
....:  [8, 10, 4, 0, 9, 3, 7, 0, 9, 10, 4, 6, 1, 3, 8, 7, 0, 9, 7],
....:  [7, 5, 5, 0, 9, 10, 4, 0, 9, 3, 3, 7, 0, 9, 7, 5, 0, 9, 3],
....:  [3, 7, 6, 1, 10, 4, 5, 0, 9, 8, 10, 4, 0, 9, 3, 7, 0, 9, 10],
....:  [10, 4, 6, 1, 3, 3, 7, 0, 9, 7, 5, 5, 0, 9, 10, 4, 0, 9, 3],
....:  [2, 5, 6, 1, 8, 10, 4, 0, 9, 3, 7, 6, 1, 10, 4, 5, 0, 9, 8],
....:  [8, 7, 6, 1, 7, 5, 5, 0, 9, 10, 4, 6, 1, 3, 3, 7, 0, 9, 7],
....:  [7, 5, 6, 1, 3, 7, 6, 1, 10, 4, 5, 6, 1, 8, 10, 4, 0, 9, 3]]

The above patch have been chosen among 1000 other randomly generated as the closest to the asymptotic frequencies of the tiles in Jeandel-Rao tilings (or at least in the minimal subshift that I describe in the preprint):

sage: from collections import Counter
sage: c = Counter(flatten(data))
sage: tile_count = [c[i] for i in range(11)]

The asymptotic frequencies:

sage: phi = golden_ratio.n()
sage: Linv = [2*phi + 6, 2*phi + 6, 18*phi + 10, 2*phi + 6, 8*phi + 2,
....:      5*phi + 4, 2*phi + 6, 12/5*phi + 14/5, 8*phi + 2,
....:      2*phi + 6, 8*phi + 2]
sage: perfect_proportions = vector([1/a for a in Linv])

Comparison of the number of tiles of each type with the expected frequency:

sage: header_row = ['tile id', 'Asymptotic frequency', 'Expected nb of copies',
....:               'Nb copies in the 33x19 patch']
sage: columns = [range(11), perfect_proportions, vector(perfect_proportions)*33*19, tile_count]
sage: table(columns=columns, header_row=header_row)
  tile id   Asymptotic frequency   Expected nb of copies   Nb copies in the 33x19 patch
+---------+----------------------+-----------------------+------------------------------+
  0         0.108271182329550      67.8860313206280        67
  1         0.108271182329550      67.8860313206280        65
  2         0.0255593590340479     16.0257181143480        16
  3         0.108271182329550      67.8860313206280        71
  4         0.0669152706817991     41.9558747174880        42
  5         0.0827118232955023     51.8603132062800        51
  6         0.108271182329550      67.8860313206280        65
  7         0.149627093977301      93.8161879237680        95
  8         0.0669152706817991     41.9558747174880        44
  9         0.108271182329550      67.8860313206280        67
  10        0.0669152706817991     41.9558747174880        44

I brought the \(33\times19=641\) tiles at the conference and offered to the first 7 persons to find a \(7\times 7\) tiling the opportunity to keep the 49 tiles they used. 49 is a good number since the frequency of the lowest tile (with id 2) is about 2% which allows to have at least one copy of each tile in a subset of 49 tiles allowing a solution.

A natural question to ask is how many such \(7\times 7\) tilings does there exist? With ticket #25125 that was merged in Sage 8.3 this Spring, it is possible to enumerate and count solutions in parallel with Knuth dancing links algorithm. After the installation of the Sage Optional package slabbe (sage -pip install slabbe), one may compute that there are 152244 solutions.

sage: from slabbe import WangTileSet
sage: tiles = [(2,4,2,1), (2,2,2,0), (1,1,3,1), (1,2,3,2), (3,1,3,3),
....: (0,1,3,1), (0,0,0,1), (3,1,0,2), (0,2,1,2), (1,2,1,4), (3,3,1,2)]
sage: T0 = WangTileSet(tiles)
sage: T0_solver = T0.solver(7,7)
sage: %time T0_solver.number_of_solutions(ncpus=8)
CPU times: user 16 ms, sys: 82.3 ms, total: 98.3 ms
Wall time: 388 ms
152244

One may also get the list of all solutions and print one of them:

sage: %time L = T0_solver.all_solutions(); print(len(L))
152244
CPU times: user 6.46 s, sys: 344 ms, total: 6.8 s
Wall time: 6.82 s
sage: L[0]
A wang tiling of a 7 x 7 rectangle
sage: L[0].table()  # warning: the output is in Cartesian-like coordinates
[[1, 8, 10, 4, 5, 0, 9],
 [1, 7, 2, 5, 6, 1, 8],
 [1, 3, 8, 7, 6, 1, 7],
 [0, 9, 7, 5, 6, 1, 3],
 [0, 9, 3, 7, 6, 1, 8],
 [1, 8, 10, 4, 6, 1, 7],
 [1, 7, 2, 2, 6, 1, 3]]

This is the number of distinct sets of 49 tiles which admits a 7x7 solution:

sage: from collections import Counter
sage: def count_tiles(tiling):
....:     C = Counter(flatten(tiling.table()))
....:     return tuple(C.get(a,0) for a in range(11))
sage: Lfreq = map(count_tiles, L)
sage: Lfreq_count = Counter(Lfreq)
sage: len(Lfreq_count)
83258

Number of other solutions with the same set of 49 tiles:

sage: Counter(Lfreq_count.values())
Counter({1: 49076, 2: 19849, 3: 6313, 4: 3664, 6: 1410, 5: 1341, 7: 705, 8:
293, 9: 159, 14: 116, 10: 104, 12: 97, 18: 44, 11: 26, 15: 24, 13: 10, 17: 8,
22: 6, 32: 6, 16: 3, 28: 2, 19: 1, 21: 1})

How the number of \(k\times k\)-solutions grows for k from 0 to 9:

sage: [T0.solver(k,k).number_of_solutions() for k in range(10)]
[0, 11, 85, 444, 1723, 9172, 50638, 152244, 262019, 1641695]

Unfortunately, most of those \(k\times k\)-solutions are not extendable to a tiling of the whole plane. Indeed the number of \(k\times k\) patches in the language of the minimal aperiodic subshift that I am able to describe and which is a proper subset of Jeandel-Rao tilings seems, according to some heuristic, to be something like:

[1, 11, 49, 108, 184, 268, 367, 483]

I do not share my (ugly) code for this computation yet, as I will rather share clean code soon when times come. So among the 152244 about only 483 (0.32%) of them are prolongable into a uniformly recurrent tiling of the plane.

A time evolution picture of packages built in parallel by Sage

2016-12-16T16:13:00Z

Compiling sage takes a while and does a lot of stuff. Each time I am wondering which components takes so much time and which are fast. I wrote a module in my slabbe version 0.3b2 package available on PyPI to figure this out.

This is after compiling 7.5.beta6 after an upgrade from 7.5.beta4:

sage: from slabbe.analyze_sage_build import draw_sage_build
sage: draw_sage_build().pdf()

From scratch from a fresh git clone of 7.5.beta6, after running MAKE='make -j4' make ptestlong, I get:

sage: from slabbe.analyze_sage_build import draw_sage_build
sage: draw_sage_build().pdf()

The picture does not include the start and ptestlong because there was an error compiling the documentation.

By default, draw_sage_build considers all of the logs files in logs/pkgs but options are available to consider only log files created in a given interval of time. See draw_sage_build? for more info.

unsupported operand parent for *, Matrix over number field, vector over symbolic ring

2016-02-18T10:17:00Z

Yesterday I received this email (in french):

Salut,
avec Thomas on a une question bête:

K.=NumberField(x*x-x-1)

J'aimerais multiplier une matrice avec des coefficients en x par un vecteur
contenant des variables a et b.  Il dit "unsupported operand parent for *,
Matrix over number field, vector over symbolic ring"

Est ce grave ?

Here is my answer. Indeed, in Sage, symbolic variables can't multiply with elements in an Number Field in x:

sage: x = var('x')
sage: K.<x> = NumberField(x*x-x-1)
sage: a = var('a')
sage: a*x
Traceback (most recent call last)
...
TypeError: unsupported operand parent(s) for '*': 'Symbolic Ring' and
'Number Field in x with defining polynomial x^2 - x - 1'

But, we can define a polynomial ring with variables in a,b and coefficients in the NumberField. Then, we are able to multiply a with x:

sage: x = var('x')
sage: K.<x> = NumberField(x*x-x-1)
sage: K
Number Field in x with defining polynomial x^2 - x - 1
sage: R.<a,b> = K['a','b']
sage: R
Multivariate Polynomial Ring in a, b over Number Field in x with
defining polynomial x^2 - x - 1
sage: a*x
(x)*a

With two square brackets, we obtain powers series:

sage: R.<a,b> = K[['a','b']]
sage: R
Multivariate Power Series Ring in a, b over Number Field in x with
defining polynomial x^2 - x - 1
sage: a*x*b
(x)*a*b

It works with matrices:

sage: MS = MatrixSpace(R,2,2)
sage: MS
Full MatrixSpace of 2 by 2 dense matrices over Multivariate Power
Series Ring in a, b over Number Field in x with defining polynomial
x^2 - x - 1
sage: MS([0,a,b,x])
[  0   a]
[  b (x)]
sage: m1 = MS([0,a,b,x])
sage: m2 = MS([0,a+x,b*b+x,x*x])
sage: m1 + m2 * m1
[              (x)*b + a*b       (x + 1) + (x + 1)*a]
[                (x + 2)*b (3*x + 1) + (x)*a + a*b^2]

slabbe-0.2.spkg released

2015-11-30T11:53:00Z

These is a summary of the functionalities present in slabbe-0.2.spkg optional Sage package. It works on version 6.8 of Sage but will work best with sage-6.10 (it is using the new code for cartesian_product merged the the betas of sage-6.10). It contains 7 new modules:

finite_word.py

language.py

lyapunov.py

matrix_cocycle.py

mult_cont_frac.pyx

ranking_scale.py

tikz_picture.py

Cheat Sheets

The best way to have a quick look at what can be computed with the optional Sage package slabbe-0.2.spkg is to look at the 3-dimensional Continued Fraction Algorithms Cheat Sheets available on the arXiv since today. It gathers a handful of informations on different 3-dimensional Continued Fraction Algorithms including well-known and old ones (Poincaré, Brun, Selmer, Fully Subtractive) and new ones (Arnoux-Rauzy-Poincaré, Reverse, Cassaigne).

Installation

sage -i http://www.slabbe.org/Sage/slabbe-0.2.spkg    # on sage 6.8
sage -p http://www.slabbe.org/Sage/slabbe-0.2.spkg    # on sage 6.9 or beyond

Examples

Computing the orbit of Brun algorithm on some input in \(\mathbb{R}^3_+\) including dual coordinates:

sage: from slabbe.mult_cont_frac import Brun
sage: algo = Brun()
sage: algo.cone_orbit_list((100, 87, 15), 4)
[(13.0, 87.0, 15.0, 1.0, 2.0, 1.0, 321),
 (13.0, 72.0, 15.0, 1.0, 2.0, 3.0, 132),
 (13.0, 57.0, 15.0, 1.0, 2.0, 5.0, 132),
 (13.0, 42.0, 15.0, 1.0, 2.0, 7.0, 132)]

Computing the invariant measure:

sage: fig = algo.invariant_measure_wireframe_plot(n_iterations=10^6, ndivs=30)
sage: fig.savefig('a.png')

Drawing the cylinders:

sage: cocycle = algo.matrix_cocycle()
sage: t = cocycle.tikz_n_cylinders(3, scale=3)
sage: t.png()

Computing the Lyapunov exponents of the 3-dimensional Brun algorithm:

sage: from slabbe.lyapunov import lyapunov_table
sage: lyapunov_table(algo, n_orbits=30, n_iterations=10^7)
  30 succesful orbits     min       mean      max       std
+-----------------------+---------+---------+---------+---------+
  $\theta_1$              0.3026    0.3045    0.3051    0.00046
  $\theta_2$              -0.1125   -0.1122   -0.1115   0.00020
  $1-\theta_2/\theta_1$   1.3680    1.3684    1.3689    0.00024

Dealing with tikzpictures

Since I create lots of tikzpictures in my code and also because I was unhappy at how the view command of Sage handles them (a tikzpicture is not a math expression to put inside dollar signs), I decided to create a class for tikzpictures. I think this module could be useful in Sage so I will propose its inclusion soon.

I am using the standalone document class which allows some configurations like the border:

sage: from slabbe import TikzPicture
sage: g = graphs.PetersenGraph()
sage: s = latex(g)
sage: t = TikzPicture(s, standalone_configs=["border=4mm"], packages=['tkz-graph'])

The repr method does not print all of the string since it is often very long. Though it shows how many lines are not printed:

sage: t
\documentclass[tikz]{standalone}
\standaloneconfig{border=4mm}
\usepackage{tkz-graph}
\begin{document}
\begin{tikzpicture}
%
\useasboundingbox (0,0) rectangle (5.0cm,5.0cm);
%
\definecolor{cv0}{rgb}{0.0,0.0,0.0}
...
... 68 lines not printed (3748 characters in total) ...
...
\Edge[lw=0.1cm,style={color=cv6v8,},](v6)(v8)
\Edge[lw=0.1cm,style={color=cv6v9,},](v6)(v9)
\Edge[lw=0.1cm,style={color=cv7v9,},](v7)(v9)
%
\end{tikzpicture}
\end{document}

There is a method to generates a pdf and another for generating a png. Both opens the file in a viewer by default unless view=False:

sage: pathtofile = t.png(density=60, view=False)
sage: pathtofile = t.pdf()

Compare this with the output of view(s, tightpage=True) which does not allow to control the border and also creates a second empty page on some operating system (osx, only one page on ubuntu):

sage: view(s, tightpage=True)

One can also provide the filename where to save the file in which case the file is not open in a viewer:

sage: _ = t.pdf('petersen_graph.pdf')

Another example with polyhedron code taken from this Sage thematic tutorial Draw polytopes in LateX using TikZ:

sage: V = [[1,0,1],[1,0,0],[1,1,0],[0,0,-1],[0,1,0],[-1,0,0],[0,1,1],[0,0,1],[0,-1,0]]
sage: P = Polyhedron(vertices=V).polar()
sage: s = P.projection().tikz([674,108,-731],112)
sage: t = TikzPicture(s)
sage: t
\documentclass[tikz]{standalone}
\begin{document}
\begin{tikzpicture}%
        [x={(0.249656cm, -0.577639cm)},
        y={(0.777700cm, -0.358578cm)},
        z={(-0.576936cm, -0.733318cm)},
        scale=2.000000,
...
... 80 lines not printed (4889 characters in total) ...
...
\node[vertex] at (1.00000, 1.00000, -1.00000)     {};
\node[vertex] at (1.00000, 1.00000, 1.00000)     {};
%%
%%
\end{tikzpicture}
\end{document}
sage: _ = t.pdf()

There are 13.366.431.646 solutions to the Quantumino game

2015-09-21T14:55:00Z

Some years ago, I wrote code in Sage to solve the Quantumino puzzle. I also used it to make a one-minute video illustrating the Dancing links algorithm which I am proud to say it is now part of the Dancing links wikipedia page.

Let me recall that the goal of the Quantumino puzzle is to fill a \(2\times 5\times 8\) box with 16 out of 17 three-dimensional pentaminos. After writing the sage code to solve the puzzle, one question was left: how many solutions are there? Is the official website realist or very prudent when they say that there are over 10.000 potential solutions? Can it be computed in hours? days? months? years? The only thing I knew was that the following computation (letting the 0-th pentamino aside) never finished on my machine:

sage: from sage.games.quantumino import QuantuminoSolver
sage: QuantuminoSolver(0).number_of_solutions()   # long time :)

Since I spent already too much time on this side-project, I decided in 2012 to stop investing any more time on it and to really focus on finishing writing my thesis.

So before I finish writing my thesis, I knew that the computation was not going to take a light-year, since I was able to finish the computation of the number of solutions when the 0-th pentamino is put aside and when one pentamino is pre-positioned somewhere in the box. That computation completed in 4 hours on my old laptop and gave about 5 millions solutions. There are 17 choices of pentatminos to put aside, there are 360 distinct positions of that pentamino in the box, so I estimated the number of solution to be something like \(17\times 360\times 5000000 = 30 \times 10^9\). Most importantly, I estimated the computation to take \(17\times 360\times 4= 24480\) hours or 1020 days. Therefore, I knew I could not do it on my laptop.

But last year, I received an email from the designer of the Quantumino puzzle:

-------- Message transféré --------
Sujet : quantumino
Date : Tue, 09 Dec 2014 13:22:30 +0100
De : Nicolaas Neuwahl
Pour : Sebastien Labbe

hi sébastien labbé,

i'm the designer of the quantumino puzzle.
i'm not a mathematician, i'm an architect. i like mathematics.
i'm quite impressed to see the sage work on quantumino, also i have not the
knowledge for full understanding.

i have a question for you - can you tell me HOW MANY different quantumino-
solutions exist?

ty and bye

nicolaas neuwahl

This summer was a good timing to launch the computation on my beautiful Intel® Core™ i5-4590 CPU @ 3.30GHz × 4 at Université de Liège. First, I improved the Sage code to allow a parallel computation of number of solutions in the dancing links code (#18987, merged in a Sage 6.9.beta6). Secondly, we may remark that each tiling of the \(2\times 5\times 8\) box can be rotated in order to find 3 other solutions. It is possible to gain a factor 4 by avoiding to count 4 times the same solution up to rotations (#19107, still needs work from myself). Thanks to Vincent Delecroix for doing the review on both ticket. Dividing the estimated 1024 days of computation needed by a factor \(4\times 4=16\) gives an approximation of 64 days to complete the computation. Two months, just enough to be tractable!

With those two tickets (some previous version to be honest) on top of sage-6.8, I started the computation on August 4th and the computation finished last week on September 18th for a total of 45 days. The computation was stopped only once on September 8th (I forgot to close firefox and thunderbird that night...).

The number of solutions and computation time for each pentamino put aside together with the first solution found is shown in the table below. We remark that some values are equal when the aside pentaminoes are miror images (why!?:).


634 900 493 solutions	634 900 493 solutions
2 days, 6:22:44.883358	2 days, 6:19:08.945691

509 560 697 solutions	509 560 697 solutions
2 days, 0:01:36.844612	2 days, 0:41:59.447773

628 384 422 solutions	628 384 422 solutions
2 days, 7:52:31.459247	2 days, 8:44:49.465672

1 212 362 145 solutions	1 212 362 145 solutions
3 days, 17:25:00.346627	3 days, 19:10:02.353063

197 325 298 solutions	556 534 800 solutions
22:51:54.439932	1 day, 19:05:23.908326

664 820 756 solutions	468 206 736 solutions
2 days, 8:48:54.767662	1 day, 20:14:56.014557

1 385 955 043 solutions	1 385 955 043 solutions
4 days, 1:40:30.270929	4 days, 4:44:05.399367

694 998 374 solutions	694 998 374 solutions
2 days, 11:44:29.631	2 days, 6:01:57.946708

1 347 221 708 solutions
3 days, 21:51:29.043459

Therefore the total number of solutions up to rotations is 13 366 431 646 which is indeed more than 10000:)

sage: L = [634900493, 634900493, 509560697, 509560697, 628384422,
628384422, 1212362145, 1212362145, 197325298, 556534800, 664820756,
468206736, 1385955043, 1385955043, 694998374, 694998374, 1347221708]
sage: sum(L)
13366431646
sage: factor(_)
2 * 23 * 271 * 1072231

Summary
The machine (4 cores)	Intel® Core™ i5-4590 CPU @ 3.30GHz × 4 (Université de Liège)
Computation Time	45 days, (Aug 4th -- Sep 18th, 2015)
Number of solutions (up to rotations)	13 366 431 646
Number of solutions / cpu / second	859

My code will be available on github.

About the video on wikipedia.

I must say that the video is not perfect. On wikipedia, the file talk page of the video says that the Jerky camera movement is distracting. That is because I managed to make the video out of images created by .show(viewer='tachyon') which changes the coordinate system, hardcodes a lot of parameters, zoom properly, simplifies stuff to make sure the user don't see just a blank image. But, for making a movie, we need access to more parameters especially the placement of the camera (to avoid the jerky movement). I know that Tachyon allows all of that. It is still a project that I have to create a more versatile Graphics3D -> Tachyon conversion allowing to construct nice videos of evolving mathematical objects. That's another story.

Arnoux-Rauzy-Poincaré sequences

2015-02-26T16:22:00Z

In a recent article with Valérie Berthé [BL15], we provided a multidimensional continued fraction algorithm called Arnoux-Rauzy-Poincaré (ARP) to construct, given any vector \(v\in\mathbb{R}_+^3\), an infinite word \(w\in\{1,2,3\}^\mathbb{N}\) over a three-letter alphabet such that the frequencies of letters in \(w\) exists and are equal to \(v\) and such that the number of factors (i.e. finite block of consecutive letters) of length \(n\) appearing in \(w\) is linear and less than \(\frac{5}{2}n+1\). We also conjecture that for almost all \(v\) the contructed word describes a discrete path in the positive octant staying at a bounded distance from the euclidean line of direction \(v\).

In Sage, you can construct this word using the next version of my package slabbe-0.2 (not released yet, email me to press me to finish it). The one with frequencies of letters proportionnal to \((1, e, \pi)\) is:

sage: from slabbe.mcf import algo
sage: D = algo.arp.substitutions()
sage: it = algo.arp.coding_iterator((1,e,pi))
sage: w = words.s_adic(it, repeat(1), D)
word: 1232323123233231232332312323123232312323...

The factor complexity is close to 2n+1 and the balance is often less or equal to three:

sage: w[:10000].number_of_factors(100)
202
sage: w[:100000].number_of_factors(1000)
2002
sage: w[:1000].balance()
3
sage: w[:2000].balance()
3

Note that bounded distance from the euclidean line almost surely was proven in [DHS2013] for Brun algorithm, another MCF algorithm.

Other approaches: Standard model and billiard sequences

Other approaches have been proposed to construct such discrete lines.

One of them is the standard model of Eric Andres [A03]. It is also equivalent to billiard sequences in the cube. It is well known that the factor complexity of billiard sequences is quadratic \(p(n)=n^2+n+1\) [AMST94]. Experimentally, we can verify this. We first create a billiard word of some given direction:

sage: from slabbe import BilliardCube
sage: v = vector(RR, (1, e, pi))
sage: b = BilliardCube(v)
sage: b
Cubic billiard of direction (1.00000000000000, 2.71828182845905, 3.14159265358979)
sage: w = b.to_word()
sage: w
word: 3231232323123233213232321323231233232132...

We create some prefixes of \(w\) that we represent internally as char*. The creation is slow because the implementation of billiard words in my optional package is in Python and is not that efficient:

sage: p3 = Word(w[:10^3], alphabet=[1,2,3], datatype='char')
sage: p4 = Word(w[:10^4], alphabet=[1,2,3], datatype='char') # takes 3s
sage: p5 = Word(w[:10^5], alphabet=[1,2,3], datatype='char') # takes 32s
sage: p6 = Word(w[:10^6], alphabet=[1,2,3], datatype='char') # takes 5min 20s

We see below that exactly \(n^2+n+1\) factors of length \(n<20\) appears in the prefix of length 1000000 of \(w\):

sage: A = ['n'] + range(30)
sage: c3 = ['p_(w[:10^3])(n)'] + map(p3.number_of_factors, range(30))
sage: c4 = ['p_(w[:10^4])(n)'] + map(p4.number_of_factors, range(30))
sage: c5 = ['p_(w[:10^5])(n)'] + map(p5.number_of_factors, range(30)) # takes 4s
sage: c6 = ['p_(w[:10^6])(n)'] + map(p6.number_of_factors, range(30)) # takes 49s
sage: ref = ['n^2+n+1'] + [n^2+n+1 for n in range(30)]
sage: T = table(columns=[A,c3,c4,c5,c6,ref])
sage: T
  n    p_(w[:10^3])(n)   p_(w[:10^4])(n)   p_(w[:10^5])(n)   p_(w[:10^6])(n)   n^2+n+1
+----+-----------------+-----------------+-----------------+-----------------+---------+
  0    1                 1                 1                 1                 1
  1    3                 3                 3                 3                 3
  2    7                 7                 7                 7                 7
  3    13                13                13                13                13
  4    21                21                21                21                21
  5    31                31                31                31                31
  6    43                43                43                43                43
  7    52                55                56                57                57
  8    63                69                71                73                73
  9    74                85                88                91                91
  10   87                103               107               111               111
  11   100               123               128               133               133
  12   115               145               151               157               157
  13   130               169               176               183               183
  14   144               195               203               211               211
  15   160               223               232               241               241
  16   176               253               263               273               273
  17   192               285               296               307               307
  18   208               319               331               343               343
  19   224               355               368               381               381
  20   239               392               407               421               421
  21   254               430               448               463               463
  22   268               470               491               507               507
  23   282               510               536               553               553
  24   296               552               583               601               601
  25   310               596               632               651               651
  26   324               642               683               703               703
  27   335               687               734               757               757
  28   345               734               787               813               813
  29   355               783               842               871               871

Billiard sequences generate paths that are at a bounded distance from an euclidean line. This is equivalent to say that the balance is finite. The balance is defined as the supremum value of difference of the number of apparition of a letter in two factors of the same length. For billiard sequences, the balance is 2:

sage: p3.balance()
2
sage: p4.balance() # takes 2min 37s
2

Other approaches: Melançon and Reutenauer

Melançon and Reutenauer [MR13] also suggested a method that generalizes Christoffel words in higher dimension. The construction is based on the application of two substitutions generalizing the construction of sturmian sequences. Below we compute the factor complexity and the balance of some of their words over a three-letter alphabet.

On a three-letter alphabet, the two morphisms are:

sage: L = WordMorphism('1->1,2->13,3->2')
sage: R = WordMorphism('1->13,2->2,3->3')
sage: L
WordMorphism: 1->1, 2->13, 3->2
sage: R
WordMorphism: 1->13, 2->2, 3->3

Example 1: periodic case \(LRLRLRLRLR\dots\). In this example, the factor complexity seems to be around \(p(n)=2.76n\) and the balance is at least 28:

sage: from itertools import repeat, cycle
sage: W = words.s_adic(cycle((L,R)),repeat('1'))
sage: W
word: 1213122121313121312212212131221213131213...
sage: map(W[:10000].number_of_factors, [10,20,40,80])
[27, 54, 110, 221]
sage: [27/10., 54/20., 110/40., 221/80.]
[2.70000000000000, 2.70000000000000, 2.75000000000000, 2.76250000000000]
sage: W[:1000].balance()  # takes 1.6s
21
sage: W[:2000].balance()  # takes 6.4s
28

Example 2: \(RLR^2LR^4LR^8LR^{16}LR^{32}LR^{64}LR^{128}\dots\) taken from the conclusion of their article. In this example, the factor complexity seems to be \(p(n)=3n\) and balance at least as high (=bad) as \(122\):

sage: W = words.s_adic([R,L,R,R,L,R,R,R,R,L]+[R]*8+[L]+[R]*16+[L]+[R]*32+[L]+[R]*64+[L]+[R]*128,'1')
sage: W.length()
330312
sage: map(W.number_of_factors, [10, 20, 100, 200, 300, 1000])
[29, 57, 295, 595, 895, 2981]
sage: [29/10., 57/20., 295/100., 595/200., 895/300., 2981/1000.]
[2.90000000000000,
 2.85000000000000,
 2.95000000000000,
 2.97500000000000,
 2.98333333333333,
 2.98100000000000]
sage: W[:1000].balance()  # takes 1.6s
122
sage: W[:2000].balance()  # takes 6s
122

Example 3: some random ones. The complexity \(p(n)/n\) occillates between 2 and 3 for factors of length \(n=1000\) in prefixes of length 100000:

sage: for _ in range(10):
....:     W = words.s_adic([choice((L,R)) for _ in range(50)],'1')
....:     print W[:100000].number_of_factors(1000)/1000.
2.02700000000000
2.23600000000000
2.74000000000000
2.21500000000000
2.78700000000000
2.52700000000000
2.85700000000000
2.33300000000000
2.65500000000000
2.51800000000000

For ten randomly generated words, the balance goes from 6 to 27 which is much more than what is obtained for billiard words or by our approach:

sage: for _ in range(10):
....:     W = words.s_adic([choice((L,R)) for _ in range(50)],'1')
....:     print W[:1000].balance(), W[:2000].balance()
12 15
8 24
14 14
5 11
17 17
14 14
6 6
19 27
9 16
12 12

References

[BL15]

V. Berthé, S. Labbé, Factor Complexity of S-adic words generated by the Arnoux-Rauzy-Poincaré Algorithm, Advances in Applied Mathematics 63 (2015) 90-130. http://dx.doi.org/10.1016/j.aam.2014.11.001

[DHS2013]

Delecroix, Vincent, Tomás Hejda, and Wolfgang Steiner. “Balancedness of Arnoux-Rauzy and Brun Words.” In Combinatorics on Words, 119–31. Springer, 2013. http://link.springer.com/chapter/10.1007/978-3-642-40579-2_14.

[A03]

E. Andres, Discrete linear objects in dimension n: the standard model, Graphical Models 65 (2003) 92-111.

[AMST94]

P. Arnoux, C. Mauduit, I. Shiokawa, J. I. Tamura, Complexity of sequences defined by billiards in the cube, Bull. Soc. Math. France 122 (1994) 1-12.

[MR13]

G. Melançon, C. Reutenauer, On a class of Lyndon words extending Christoffel words and related to a multidimensional continued fraction algorithm. J. Integer Seq. 16, No. 9, Article 13.9.7, 30 p., electronic only (2013). https://cs.uwaterloo.ca/journals/JIS/VOL16/Reutenauer/reut3.html

Abelian complexity of the Oldenburger sequence

2014-09-27T22:00:00Z

The Oldenburger infinite sequence [O39] \[ K = 1221121221221121122121121221121121221221\ldots \] also known under the name of Kolakoski, is equal to its exponent trajectory. The exponent trajectory \(\Delta\) can be obtained by counting the lengths of blocks of consecutive and equal letters: \[ K = 1^12^21^22^11^12^21^12^21^22^11^22^21^12^11^22^11^12^21^22^11^22^11^12^21^12^21^22^11^12^21^12^11^22^11^22^21^12^21^2\ldots \] The sequence of exponents above gives the exponent trajectory of the Oldenburger sequence: \[ \Delta = 12211212212211211221211212\ldots \] which is equal to the original sequence \(K\). You can define this sequence in Sage:

sage: K = words.KolakoskiWord()
sage: K
word: 1221121221221121122121121221121121221221...
sage: K.delta()          # delta returns the exponent trajectory
word: 1221121221221121122121121221121121221221...

There are a lot of open problem related to basic properties of that sequence. For example, we do not know if that sequence is recurrent, that is, all finite subword or factor (finite block of consecutive letters) always reappear. Also, it is still open to prove whether the density of 1 in that sequence is equal to \(1/2\).

In this blog post, I do some computations on its abelian complexity \(p_{ab}(n)\) defined as the number of distinct abelian vectors of subwords of length \(n\) in the sequence. The abelian vector \(\vec{w}\) of a word \(w\) counts the number of occurences of each letter: \[ w = 12211212212 \quad \mapsto \quad 1^5 2^7 \text{, abelianized} \quad \mapsto \quad \vec{w} = (5, 7) \text{, the abelian vector of } w \]

Here are the abelian vectors of subwords of length 10 and 20 in the prefix of length 100 of the Oldenburger sequence. The functions abelian_vectors and abelian_complexity are not in Sage as of now. Code is available at trac #17058 to be merged in Sage soon:

sage: prefix = words.KolakoskiWord()[:100]
sage: prefix.abelian_vectors(10)
{(4, 6), (5, 5), (6, 4)}
sage: prefix.abelian_vectors(20)
{(8, 12), (9, 11), (10, 10), (11, 9), (12, 8)}

Therefore, the prefix of length 100 has 3 vectors of subwords of length 10 and 5 vectors of subwords of length 20:

sage: p100.abelian_complexity(10)
3
sage: p100.abelian_complexity(20)
5

I import the OldenburgerSequence from my optional spkg because it is faster than the implementation in Sage:

sage: from slabbe import KolakoskiWord as OldenburgerSequence
sage: Olden = OldenburgerSequence()

I count the number of abelian vectors of subwords of length 100 in the prefix of length \(2^{20}\) of the Oldenburger sequence:

sage: prefix = Olden[:2^20]
sage: %time prefix.abelian_vectors(100)
CPU times: user 3.48 s, sys: 66.9 ms, total: 3.54 s
Wall time: 3.56 s
{(47, 53), (48, 52), (49, 51), (50, 50), (51, 49), (52, 48), (53, 47)}

Number of abelian vectors of subwords of length less than 100 in the prefix of length \(2^{20}\) of the Oldenburger sequence:

sage: %time L100 = map(prefix.abelian_complexity, range(100))
CPU times: user 3min 20s, sys: 1.08 s, total: 3min 21s
Wall time: 3min 23s
sage: from collections import Counter
sage: Counter(L100)
Counter({5: 26, 6: 26, 4: 17, 7: 15, 3: 8, 8: 4, 2: 3, 1: 1})

Let's draw that:

sage: labels = ('Length of factors', 'Number of abelian vectors')
sage: title = 'Abelian Complexity of the prefix of length $2^{20}$ of Oldenburger sequence'
sage: list_plot(L100, color='green', plotjoined=True, axes_labels=labels, title=title)

It seems to grow something like \(\log(n)\). Let's now consider subwords of length \(2^n\) for \(0\leq n\leq 12\) in the same prefix of length \(2^{20}\):

sage: %time L20 = [(2^n, prefix.abelian_complexity(2^n)) for n in range(20)]
CPU times: user 41 s, sys: 239 ms, total: 41.2 s
Wall time: 41.5 s
sage: L20
[(1, 2), (2, 3), (4, 3), (8, 3), (16, 3), (32, 5), (64, 5), (128, 9),
(256, 9), (512, 13), (1024, 17), (2048, 22), (4096, 27), (8192, 40),
(16384, 46), (32768, 67), (65536, 81), (131072, 85), (262144, 90), (524288, 104)]

I now look at subwords of length \(2^n\) for \(0\leq n\leq 23\) in the longer prefix of length \(2^{24}\):

sage: prefix = Olden[:2^24]
sage: %time L24 = [(2^n, prefix.abelian_complexity(2^n)) for n in range(24)]
CPU times: user 20min 47s, sys: 13.5 s, total: 21min
Wall time: 20min 13s
sage: L24
[(1, 2), (2, 3), (4, 3), (8, 3), (16, 3), (32, 5), (64, 5), (128, 9), (256,
9), (512, 13), (1024, 17), (2048, 23), (4096, 33), (8192, 46), (16384, 58),
(32768, 74), (65536, 98), (131072, 134), (262144, 165), (524288, 229),
(1048576, 302), (2097152, 371), (4194304, 304), (8388608, 329)]

The next graph gather all of the above computations:

sage: G = Graphics()
sage: legend = 'in the prefix of length 2^{}'
sage: G += list_plot(L24, plotjoined=True, thickness=4, color='blue', legend_label=legend.format(24))
sage: G += list_plot(L20, plotjoined=True, thickness=4, color='red', legend_label=legend.format(20))
sage: G += list_plot(L100, plotjoined=True, thickness=4, color='green', legend_label=legend.format(20))
sage: labels = ('Length of factors', 'Number of abelian vectors')
sage: title = 'Abelian complexity of Oldenburger sequence'
sage: G.show(scale=('semilogx', 2), axes_labels=labels, title=title)

A linear growth in the above graphics with logarithmic \(x\) abcisse would mean a growth in \(\log(n)\). After those experimentations, my hypothesis is that the abelian complexity of the Oldenburger sequence grows like \(\log(n)^2\).

References

[O39]

Oldenburger, Rufus (1939). "Exponent trajectories in symbolic dynamics". Transactions of the American Mathematical Society 46: 453–466. doi:10.2307/1989933

slabbe-0.1.spkg released

2014-08-27T16:53:00Z

These is a summary of the functionalities present in slabbe-0.1 optional Sage package. It depends on version 6.3 of Sage because it uses RecursivelyEnumeratedSet code that was merged in 6.3. It contains modules on digital geometry, combinatorics on words and more.

Install the optional spkg (depends on sage-6.3):

sage -i http://www.liafa.univ-paris-diderot.fr/~labbe/Sage/slabbe-0.1.spkg

In each of the example below, you first have to import the module once and for all:

sage: from slabbe import *

To construct the image below, make sure to use tikz package so that view is able to compile tikz code when called:

sage: latex.add_to_preamble("\\usepackage{tikz}")
sage: latex.extra_preamble()
'\\usepackage{tikz}'

Draw the part of a discrete plane

sage: p = DiscretePlane([1,pi,7], 1+pi+7, mu=0)
sage: d = DiscreteTube([-5,5],[-5,5])
sage: I = p & d
sage: I
Intersection of the following objects:
Set of points x in ZZ^3 satisfying: 0 <= (1, pi, 7) . x + 0 < pi + 8
DiscreteTube: Preimage of [-5, 5] x [-5, 5] by a 2 by 3 matrix
sage: clip = d.clip()
sage: tikz = I.tikz(clip=clip)
sage: view(tikz, tightpage=True)

Draw the part of a discrete line

sage: L = DiscreteLine([-2,3], 5)
sage: b = DiscreteBox([0,10], [0,10])
sage: I = L & b
sage: I
Intersection of the following objects:
Set of points x in ZZ^2 satisfying: 0 <= (-2, 3) . x + 0 < 5
[0, 10] x [0, 10]
sage: I.plot()

Double square tiles

This module was developped for the article on the combinatorial properties of double square tiles written with Ariane Garon and Alexandre Blondin Massé [BGL2012]. The original version of the code was written with Alexandre.

sage: D = DoubleSquare((34,21,34,21))
sage: D
Double Square Tile
  w0 = 3032321232303010303230301012101030   w4 = 1210103010121232121012123230323212
  w1 = 323030103032321232303                w5 = 101212321210103010121
  w2 = 2321210121232303232123230301030323   w6 = 0103032303010121010301012123212101
  w3 = 212323032321210121232                w7 = 030101210103032303010
(|w0|, |w1|, |w2|, |w3|) = (34, 21, 34, 21)
(d0, d1, d2, d3)         = (42, 68, 42, 68)
(n0, n1, n2, n3)         = (0, 0, 0, 0)
sage: D.plot()

sage: D.extend(0).extend(1).plot()

We have shown that using two invertible operations (called SWAP and TRIM), every double square tiles can be reduced to the unit square:

sage: D.plot_reduction()

The reduction operations are:

sage: D.reduction()
['SWAP_1', 'TRIM_1', 'TRIM_3', 'SWAP_1', 'TRIM_1', 'TRIM_3', 'TRIM_0', 'TRIM_2']

The result of the reduction is the unit square:

sage: unit_square = D.apply(D.reduction())
sage: unit_square
Double Square Tile
  w0 =     w4 =
  w1 = 3   w5 = 1
  w2 =     w6 =
  w3 = 2   w7 = 0
(|w0|, |w1|, |w2|, |w3|) = (0, 1, 0, 1)
(d0, d1, d2, d3)         = (2, 0, 2, 0)
(n0, n1, n2, n3)         = (0, NaN, 0, NaN)
sage: unit_square.plot()

Since SWAP and TRIM are invertible operations, we can recover every double square from the unit square:

sage: E = unit_square.extend(2).extend(0).extend(3).extend(1).swap(1).extend(3).extend(1).swap(1)
sage: D == E
True

Christoffel graphs

This module was developped for the article on a d-dimensional extension of Christoffel Words written with Christophe Reutenauer [LR2014].

sage: G = ChristoffelGraph((6,10,15))
sage: G
Christoffel set of edges for normal vector v=(6, 10, 15)
sage: tikz = G.tikz_kernel()
sage: view(tikz, tightpage=True)

Bispecial extension types

This module was developped for the article on the factor complexity of infinite sequences genereated by substitutions written with Valérie Berthé [BL2014].

The extension type of an ordinary bispecial factor:

sage: L = [(1,3), (2,3), (3,1), (3,2), (3,3)]
sage: E = ExtensionType1to1(L, alphabet=(1,2,3))
sage: E
  E(w)   1   2   3
   1             X
   2             X
   3     X   X   X
 m(w)=0, ordinary
sage: E.is_ordinaire()
True

Creation of a strong-weak pair of bispecial words from a neutral not ordinaire word:

sage: p23 = WordMorphism({1:[1,2,3],2:[2,3],3:[3]})
sage: e = ExtensionType1to1([(1,2),(2,3),(3,1),(3,2),(3,3)], [1,2,3])
sage: e
  E(w)   1   2   3
   1         X
   2             X
   3     X   X   X
 m(w)=0, not ord.
sage: A,B = e.apply(p23)
sage: A
  E(3w)   1   2   3
    1
    2         X   X
    3     X   X   X
 m(w)=1, not ord.
sage: B
  E(23w)   1   2   3
    1          X
    2
    3              X
 m(w)=-1, not ord.

Fast Kolakoski word

This module was written for fun. It uses cython implementation inspired from the 10 lines of C code written by Dominique Bernardi and shared during Sage Days 28 in Orsay, France, in January 2011.

sage: K = KolakoskiWord()
sage: K
word: 1221121221221121122121121221121121221221...
sage: %time K[10^5]
CPU times: user 1.56 ms, sys: 7 µs, total: 1.57 ms
Wall time: 1.57 ms
1
sage: %time K[10^6]
CPU times: user 15.8 ms, sys: 30 µs, total: 15.8 ms
Wall time: 15.9 ms
2
sage: %time K[10^8]
CPU times: user 1.58 s, sys: 2.28 ms, total: 1.58 s
Wall time: 1.59 s
1
sage: %time K[10^9]
CPU times: user 15.8 s, sys: 12.4 ms, total: 15.9 s
Wall time: 15.9 s
1

This is much faster than the Python implementation available in Sage:

sage: K = words.KolakoskiWord()
sage: %time K[10^5]
CPU times: user 779 ms, sys: 25.9 ms, total: 805 ms
Wall time: 802 ms
1

References

[BGL2012]

A. Blondin Massé, A. Garon, S. Labbé, Combinatorial properties of double square tiles, Theoretical Computer Science 502 (2013) 98-117. doi:10.1016/j.tcs.2012.10.040

[LR2014]

Labbé, Sébastien, and Christophe Reutenauer. A d-dimensional Extension of Christoffel Words. arXiv:1404.4021 (April 15, 2014).

[BL2014]

V. Berthé, S. Labbé, Factor Complexity of S-adic sequences generated by the Arnoux-Rauzy-Poincaré Algorithm. arXiv:1404.4189 (April, 2014).

Releasing slabbe, my own Sage package

2014-08-27T16:48:00Z

Since two years I wrote thousands of line of private code for my own research. Each module having between 500 and 2000 lines of code. The code which is the more clean corresponds to code written in conjunction with research articles. People who know me know that I systematically put docstrings and doctests in my code to facilitate reuse of the code by myself, but also in the idea of sharing it and eventually making it public.

I did not made that code into Sage because it was not mature enough. Also, when I tried to make a complete module go into Sage (see #13069 and #13346), then the monstrous never evolving #12224 became a dependency of the first and the second was unofficially reviewed asking me to split it into smaller chunks to make the review process easier. I never did it because I spent already too much time on it (making a module 100% doctested takes time). Also, the module was corresponding to a published article and I wanted to leave it just like that.

Getting new modules into Sage is hard

In general, the introduction of a complete new module into Sage is hard especially for beginners. Here are two examples I feel responsible for: #10519 is 4 years old and counting, the author has a new work and responsabilities; in #12996, the author was decouraged by the amount of work given by the reviewers. There is a lot of things a beginner has to consider to obtain a positive review. And even for a more advanced developper, other difficulties arise. Indeed, a module introduces a lot of new functions and it may also introduce a lot of new bugs... and Sage developpers are sometimes reluctant to give it a positive review. And if it finally gets a positive review, it is not available easily to normal users of Sage until the next release of Sage.

Releasing my own Sage package

Still I felt the need around me to make my code public. But how? There are people (a few of course but I know there are) who are interested in reproducing computations and images done in my articles. This is why I came to the idea of releasing my own Sage package containing my public research code. This way both developpers and colleagues that are user of Sage but not developpers will be able to install and use my code. This will make people more aware if there is something useful in a module for them. And if one day, somebody tells me: "this should be in Sage", then I will be able to say : "I agree! Do you want to review it?".

Old style Sage package vs New sytle git Sage package

Then I had to chose between the old and the new style for Sage packages. I did not like the new style, because

I wanted the history of my package to be independant of the history of Sage,

I wanted it to be as easy to install as sage -i slabbe,

I wanted it to work on any recent enough version of Sage,

I wanted to be able to release a new version, give it to a colleague who could install it right away without changing its own Sage (i.e., updating the checksums).

Therefore, I choose the old style. I based my work on other optional Sage packages, namely the SageManifolds spkg and the ore_algebra spkg.

Content of the initial version

The initial version of the slabbe Sage package has modules concerning four topics: Digital geometry, Combinatorics on words, Combinatorics and Python class inheritance.

For installation or for release notes of the initial version of the spkg, consult the slabbe spkg section of the Sage page of this website.

My status report at Sage Days 57 (RecursivelyEnumeratedSet)

2014-04-11T17:15:00Z

At Sage Days 57, I worked on the trac ticket #6637: standardize the interface to TransitiveIdeal and friends. My patch proposes to replace TransitiveIdeal and SearchForest by a new class called RecursivelyEnumeratedSet that would handle every case.

A set S is called recursively enumerable if there is an algorithm that enumerates the members of S. We consider here the recursively enumerated set that are described by some seeds and a successor function succ. The successor function may have some structure (symmetric, graded, forest) or not. Many kinds of iterators are provided: depth first search, breadth first search or elements of given depth.

TransitiveIdeal and TransitiveIdealGraded

Consider the permutations of \(\{1,2,3\}\) and the poset generated by the method permutohedron_succ:

sage: P = Permutations(3)
sage: d = {p:p.permutohedron_succ() for p in P}
sage: S = Poset(d)
sage: S.plot()

The TransitiveIdeal allows to generates all permutations from the identity permutation using the method permutohedron_succ as successor function:

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1,2,3])]
sage: T = TransitiveIdeal(succ, seed)
sage: list(T)
[[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 2, 1], [3, 1, 2]]

Remark that the previous ordering is neither breadth first neither depth first. It is a naive search because it stores the element to process in a set instead of a queue or a stack.

Note that the method permutohedron_succ produces a graded poset. Therefore, one may use the TransitiveIdealGraded class instead:

sage: T = TransitiveIdealGraded(succ, seed)
sage: list(T)
[[1, 2, 3], [2, 1, 3], [1, 3, 2], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

For TransitiveIdealGraded, the enumeration is breadth first search. Althougth, if you look at the code (version Sage 6.1.1 or earlier), we see that this iterator do not make use of the graded hypothesis at all because the known set remembers every generated elements:

current_level = self._generators
known = set(current_level)
depth = 0
while len(current_level) > 0 and depth <= self._max_depth:
    next_level = set()
    for x in current_level:
        yield x
        for y in self._succ(x):
            if y == None or y in known:
                continue
            next_level.add(y)
            known.add(y)
    current_level = next_level
    depth += 1
return

Timings for TransitiveIdeal

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: T = TransitiveIdeal(succ, seed)
sage: %time L = list(T)
CPU times: user 26.6 ms, sys: 1.57 ms, total: 28.2 ms
Wall time: 28.5 ms

sage: seed = [Permutation([1..8])]
sage: T = TransitiveIdeal(succ, seed)
sage: %time L = list(T)
CPU times: user 14.4 s, sys: 141 ms, total: 14.5 s
Wall time: 14.8 s

Timings for TransitiveIdealGraded

sage: seed = [Permutation([1..5])]
sage: T = TransitiveIdealGraded(succ, seed)
sage: %time L = list(T)
CPU times: user 25.3 ms, sys: 1.04 ms, total: 26.4 ms
Wall time: 27.4 ms

sage: seed = [Permutation([1..8])]
sage: T = TransitiveIdealGraded(succ, seed)
sage: %time L = list(T)
CPU times: user 14.5 s, sys: 85.8 ms, total: 14.5 s
Wall time: 14.7 s

In conlusion, use TransitiveIdeal for naive search algorithm and use TransitiveIdealGraded for breadth search algorithm. Both class do not use the graded hypothesis.

Recursively enumerated set with a graded structure

The new class RecursivelyEnumeratedSet provides all iterators for each case. The example below are for the graded case.

Depth first search iterator:

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: it_depth = R.depth_first_search_iterator()
sage: [next(it_depth) for _ in range(5)]
[[1, 2, 3, 4, 5],
 [1, 2, 3, 5, 4],
 [1, 2, 5, 3, 4],
 [1, 2, 5, 4, 3],
 [1, 5, 2, 4, 3]]

Breadth first search iterator:

sage: it_breadth = R.breadth_first_search_iterator()
sage: [next(it_breadth) for _ in range(5)]
[[1, 2, 3, 4, 5],
 [1, 3, 2, 4, 5],
 [1, 2, 4, 3, 5],
 [2, 1, 3, 4, 5],
 [1, 2, 3, 5, 4]]

Elements of given depth iterator:

sage: list(R.elements_of_depth_iterator(9))
[[5, 4, 2, 3, 1], [4, 5, 3, 2, 1], [5, 3, 4, 2, 1], [5, 4, 3, 1, 2]]
sage: list(R.elements_of_depth_iterator(10))
[[5, 4, 3, 2, 1]]

Levels (a level is a set of elements of the same depth):

sage: R.level(0)
[[1, 2, 3, 4, 5]]
sage: R.level(1)
{[1, 2, 3, 5, 4], [1, 2, 4, 3, 5], [1, 3, 2, 4, 5], [2, 1, 3, 4, 5]}
sage: R.level(2)
{[1, 2, 4, 5, 3],
 [1, 2, 5, 3, 4],
 [1, 3, 2, 5, 4],
 [1, 3, 4, 2, 5],
 [1, 4, 2, 3, 5],
 [2, 1, 3, 5, 4],
 [2, 1, 4, 3, 5],
 [2, 3, 1, 4, 5],
 [3, 1, 2, 4, 5]}
sage: R.level(3)
{[1, 2, 5, 4, 3],
 [1, 3, 4, 5, 2],
 [1, 3, 5, 2, 4],
 [1, 4, 2, 5, 3],
 [1, 4, 3, 2, 5],
 [1, 5, 2, 3, 4],
 [2, 1, 4, 5, 3],
 [2, 1, 5, 3, 4],
 [2, 3, 1, 5, 4],
 [2, 3, 4, 1, 5],
 [2, 4, 1, 3, 5],
 [3, 1, 2, 5, 4],
 [3, 1, 4, 2, 5],
 [3, 2, 1, 4, 5],
 [4, 1, 2, 3, 5]}
sage: R.level(9)
{[4, 5, 3, 2, 1], [5, 3, 4, 2, 1], [5, 4, 2, 3, 1], [5, 4, 3, 1, 2]}
sage: R.level(10)
{[5, 4, 3, 2, 1]}

Recursively enumerated set with a symmetric structure

We construct a recursively enumerated set with symmetric structure and depth first search for default enumeration algorithm:

sage: succ = lambda a: [(a[0]-1,a[1]), (a[0],a[1]-1), (a[0]+1,a[1]), (a[0],a[1]+1)]
sage: seeds = [(0,0)]
sage: C = RecursivelyEnumeratedSet(seeds, succ, structure='symmetric', algorithm='depth')
sage: C
A recursively enumerated set with a symmetric structure (depth first search)

In this case, depth first search is the default algorithm for iteration:

sage: it_depth = iter(C)
sage: [next(it_depth) for _ in range(10)]
[(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 9)]

Breadth first search. This algorithm makes use of the symmetric structure and remembers only the last two levels:

sage: it_breadth = C.breadth_first_search_iterator()
sage: [next(it_breadth) for _ in range(10)]
[(0, 0), (0, 1), (0, -1), (1, 0), (-1, 0), (-1, 1), (-2, 0), (0, 2), (2, 0), (-1, -1)]

Levels (elements of given depth):

sage: sorted(C.level(0))
[(0, 0)]
sage: sorted(C.level(1))
[(-1, 0), (0, -1), (0, 1), (1, 0)]
sage: sorted(C.level(2))
[(-2, 0), (-1, -1), (-1, 1), (0, -2), (0, 2), (1, -1), (1, 1), (2, 0)]

Timings for `RecursivelyEnumeratedSet`

We get same timings as for TransitiveIdeal but it uses less memory so it might be able to enumerate bigger sets:

sage: succ = attrcall("permutohedron_succ")
sage: seed = [Permutation([1..5])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: %time L = list(R)
CPU times: user 24.7 ms, sys: 1.33 ms, total: 26.1 ms
Wall time: 26.4 ms

sage: seed = [Permutation([1..8])]
sage: R = RecursivelyEnumeratedSet(seed, succ, structure='graded')
sage: %time L = list(R)
CPU times: user 14.5 s, sys: 70.2 ms, total: 14.5 s
Wall time: 14.6 s

Sébastien Labbé

On the bifurcation diagram proposed by Jang and Robinson

Dependencies

Jang-Robinson encoding of the Penrose 24 Wang tiles

Constructing Jang-Robinson Bifurcation diagram as a polygonal partition

Our claim

Defining the toral translations in the internal space as PETs

Let's fix the partition

Understanding the issue using edge label partitions

Fixed Edge labels partitions

Proposed partition for the encoding of the Penrose tilings into 24 Wang tiles

Wang tiles deduced from the partition and ℤ2-action

Introduction to Python/SageMath

Découpe laser du chapeau, tuile apériodique découverte récemment

Factor complexity of words generated by multidimensional continued fraction algorithms

Using Glucose SAT solver to find a tiling of a rectangle by polyominoes

Installation de Python, Jupyter et JupyterLab

Tiling a polyomino with polyominoes in SageMath

Computer experiments for the Lyapunov exponent for MCF algorithms when dimension is larger than 3

Comment installer et utiliser RISE, une extension du notebook Jupyter pour faire des présentations

Comparison of Wang tiling solvers

Wooden laser-cut Jeandel-Rao tiles

A time evolution picture of packages built in parallel by Sage

unsupported operand parent for *, Matrix over number field, vector over symbolic ring

slabbe-0.2.spkg released

There are 13.366.431.646 solutions to the Quantumino game

Arnoux-Rauzy-Poincaré sequences

References

Abelian complexity of the Oldenburger sequence

References

slabbe-0.1.spkg released

Draw the part of a discrete plane

Draw the part of a discrete line

Double square tiles

Christoffel graphs

Bispecial extension types

Fast Kolakoski word

References

Releasing slabbe, my own Sage package

My status report at Sage Days 57 (RecursivelyEnumeratedSet)

TransitiveIdeal and TransitiveIdealGraded

Timings for TransitiveIdeal

Timings for TransitiveIdealGraded

Recursively enumerated set with a graded structure

Recursively enumerated set with a symmetric structure

Timings for RecursivelyEnumeratedSet

Wang tiles deduced from the partition and ℤ²-action

Timings for `RecursivelyEnumeratedSet`